
| A. | ①②③ | B. | ③④⑤ | C. | ④⑤ | D. | ④⑤⑥ |
分析 利用因式分解的方法对①进行判断;根据二次根式有意义的条件和分母不为0对②进行判断;利用分母有理化对③进行判断;先解不等式组,再确定不等式的正数解,则可对④进行判断;根据方差的意义对⑤进行判断;根据二次函数的性质得到抛物线顶点坐标为(0,-1),与x轴的交点坐标为(-1,0),(1,0),则可利用x=-1时y=$\frac{1}{x}$=-1可判断双曲线y=$\frac{1}{x}$与抛物线y=x2-1在第四象限没有交点,于是可对⑥进行判断.
解答 解:-ax2-4a=-a(x2+4),所以①错误;
函数y=$\frac{1}{\sqrt{x-3}}$自变量取值范围是x-3>0,即x>3,所以②错误;
$\frac{1}{1-\sqrt{2}}$=-$\frac{1}{\sqrt{2}-1}$=-$\sqrt{2}$-1,所以③错误;
不等式组$\left\{\begin{array}{l}{2x+3>1}\\{5-x>2}\end{array}\right.$的解为-1<x<3,则不等式组的整数解为x=0,1,2,所以④正确;
把数据6、7、8、9、10都减去5得1、2、3、4、5,所以两组数据1、2、3、4、5与6、7、8、9、10的波动程度相同,所以⑤正确;
抛物线y=x2-1的顶点坐标为(0,-1),与x轴的交点坐标为(-1,0),(1,0),而x=-1时y=$\frac{1}{x}$=-1,则双曲线y=$\frac{1}{x}$与抛物线y=x2-1在第三象限没有交点,只在第一象限有一个交点,所以⑥正确.
故选D.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
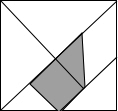 如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$.
如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
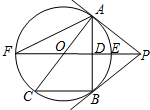 如图,PB为⊙O的切线,点B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF,
如图,PB为⊙O的切线,点B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com