
分析 (1)先算括号里面的,再算除法、加法即可;
(2)从左到右依次计算即可;
(3)先通分,再把分子相加减即可.
解答 解:(1)原式=$\frac{a(a-b)-{a}^{2}}{(a-b)^{2}}$÷$\frac{a(a-b)-{a}^{2}}{(a+b)(a-b)}$+1
=$\frac{-ab}{{(a-b)}^{2}}$•$\frac{(a+b)(a-b)}{-ab}$+1
=$\frac{a+b}{a-b}$+1
=$\frac{2a}{a-b}$;
(2)原式=$\frac{1+x+1-x}{1-{x}^{2}}$+$\frac{2}{1+{x}^{2}}$+$\frac{4}{1+{x}^{4}}$
=$\frac{2}{1-{x}^{2}}$+$\frac{2}{1+{x}^{2}}$+$\frac{4}{1+{x}^{4}}$
=$\frac{2(1+{x}^{2})+2(1-{x}^{2})}{1-{x}^{4}}$+$\frac{4}{1+{x}^{4}}$
=$\frac{4}{1-{x}^{4}}$+$\frac{4}{1+{x}^{4}}$
=$\frac{4(1+{x}^{4})+4(1-{x}^{4})}{1-{x}^{8}}$
=$\frac{8}{1-{x}^{8}}$;
(3)原式=$\frac{2}{x+3}$-$\frac{2}{x-3}$+$\frac{2x+18}{{x}^{2}-9}$
=$\frac{2(x-3)-2(x+3)+2x+18}{{x}^{2}-9}$
=$\frac{2x-6-2x-6+2x+18}{{x}^{2}-9}$
=$\frac{2(x+3)}{{x}^{2}-9}$
=$\frac{2}{x-3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
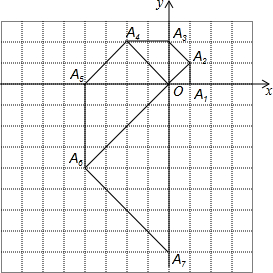 如图,O为坐标原点,点A1坐标为(1,0),以OA1为直角边作等腰直角△OA1A2,以OA2为直角边作等腰直角△OA2A3,以OA3为直角边作等腰直角△OA3A4,…,依此法继续作下去,OA2015=21007.
如图,O为坐标原点,点A1坐标为(1,0),以OA1为直角边作等腰直角△OA1A2,以OA2为直角边作等腰直角△OA2A3,以OA3为直角边作等腰直角△OA3A4,…,依此法继续作下去,OA2015=21007.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
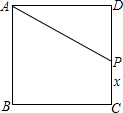 如图.正方形ABCD的边长为4cm.P为DC上的点,当点P从C向D移动时,四边形APCB的面积发生了变化.
如图.正方形ABCD的边长为4cm.P为DC上的点,当点P从C向D移动时,四边形APCB的面积发生了变化.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ③④⑤ | C. | ④⑤ | D. | ④⑤⑥ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
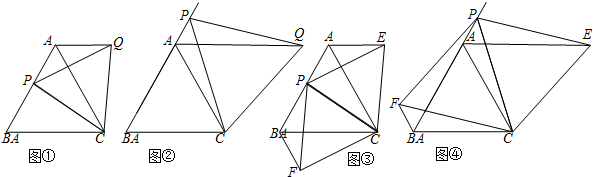
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
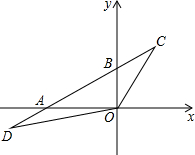 如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-4,0)、B(0,2)两点,点C、D在直线AB上,C的纵坐标为3,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-6,-1).
如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-4,0)、B(0,2)两点,点C、D在直线AB上,C的纵坐标为3,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-6,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com