
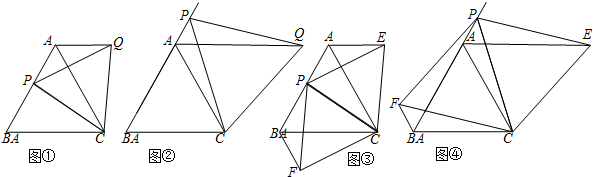
���� ��1��֤����BPC�͡�AQCȫ�ȣ����Եó�AQ=BP��ϵ��
��2��֤����BPC�͡�AQCȫ�ȣ����Եó�AQ=BP��ϵ��
��3��֤����BFC�͡�APCȫ�ȣ���PBC�͡�EACȫ�ȣ����Եó�BF=AP��BP=AE��ϵ���ٵó�AE��BF��AB֮��Ĺ�ϵ��
��4��֤����BFC�͡�APCȫ�ȣ���PBC�͡�EACȫ�ȣ����Եó�BF=AP��BP=AE��ϵ���ٵó�AE��BF��AB֮��Ĺ�ϵ��
��� �⣺��1��AQ=BP���������£�
�ߡ�ABC����CPQ�ǵȱ������Σ�
��BC=AC��CP=CQ��
���ACB=��QCP��
���PCB=��QCA��
�ڡ�BPC�͡�AQC�У�
$\left\{\begin{array}{l}{BC=AC}\\{��PCB=��QCA}\\{CP=CQ}\end{array}\right.$��
���BPC�ա�AQC��SAS����
��AQ=BP��
��2���������������£�
�ߡ�ABC����CPQ�ǵȱ������Σ�
��BC=AC��CP=CQ��
���ACB=��QCP��
���PCB=��QCA��
�ڡ�BPC�͡�AQC�У�
$\left\{\begin{array}{l}{BC=AC}\\{��PCB=��QCA}\\{CP=CQ}\end{array}\right.$��
���BPC�ա�AQC��SAS����
��AQ=BP��
��3��AE+BF=AB���������£�
�ߡ�ABC����PFC�ǵȱ������Σ�
��CF=CP��BC=AC��
���PCF=��ACB��
���BCF=��ACP��
�ڡ�PBC�͡�EAC�У�
$\left\{\begin{array}{l}{CF=CP}\\{��BCF=��ACP}\\{BC=AC}\end{array}\right.$��
���PBC�ա�EAC��SAS����
��BF=AP��
ͬ���ɵã�AE=BP��
��AB=AP+BP=BF+AE��
��4����������AE-BF=AB���������£�
�ߡ�ABC����PFC�ǵȱ������Σ�
��CF=CP��BC=AC��
���PCF=��ACB��
���BCF=��ACP��
�ڡ�PBC�͡�EAC�У�
$\left\{\begin{array}{l}{CF=CP}\\{��BCF=��ACP}\\{BC=AC}\end{array}\right.$��
���PBC�ա�EAC��SAS����
��BF=AP��
ͬ���ɵã�AE=BP��
��BP=AE=AB+AP=AB+BF��
��AE-BF=AB��
���� ������Ҫ������ȫ�������ε��ж������ʣ���������ȫ�������ε����ʵó���Ӧ��֮���ϵ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
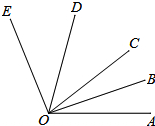 ��ͼ����AOE=100�㣬����OD��OB�ǡ�EOC����COA�Ľ�ƽ���ߣ�
��ͼ����AOE=100�㣬����OD��OB�ǡ�EOC����COA�Ľ�ƽ���ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
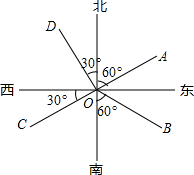 ��ͼ��ʾ�����������У���ʾ��ƫ��30����ǣ�������
��ͼ��ʾ�����������У���ʾ��ƫ��30����ǣ�������| A�� | ����OA | B�� | ����OB | C�� | ����OC | D�� | ����OD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 88.4��102 | B�� | 8.84��103 | C�� | 8.80��103 | D�� | 8.8��103 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com