
| A. | 甲乙 | B. | 甲丙 | C. | 乙丙 | D. | 丙丁 |
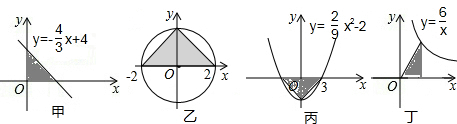
分析 甲、丙:根据函数解析式求出图象与x轴,y轴的交点坐标,再计算阴影部分的面积;
乙:可判断出阴影部分为斜边为4的等腰直角三角形,据此计算阴影部分的面积;
丁:利用反比例函数系数k的几何意义求出阴影部分的面积.
解答 解:甲:直线y=-$\frac{3}{4}$x+4与x轴交点为(3,0),与y轴的交点为(0,4),则阴影部分的面积为$\frac{1}{2}$×3×4=6;
乙:阴影部分为斜边为4的等腰直角三角形,其面积为$\frac{1}{2}$×4×2=4;
丙:抛物线y=$\frac{2}{9}{x}^{2}$-2与x轴的两个交点为(-3,0)与(3,0),顶点坐标为(0,-2),则阴影部分的面积为$\frac{1}{2}$×6×2=6;
丁:此函数是反比例函数,那么阴影部分的面积为$\frac{1}{2}$×6=3;
因此甲、丙的面积相等,
故选B.
点评 此题主要考查了函数图象与坐标轴交点坐标的求法以及图形面积的求法,是基础题,熟练掌握各类函数的图象特点是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 可以是a=-0.2,不可以是a=-2 | |
| B. | 可以是a=-2,不可以是a=-0.2 | |
| C. | 可以是a=-0.2,也可以是a=-2 | |
| D. | 既不可以是a=-0.2,也不可以是a=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
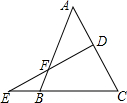 如图所示,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且$\frac{EF}{FD}$=$\frac{AC}{BC}$.求证:AD=EB.
如图所示,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且$\frac{EF}{FD}$=$\frac{AC}{BC}$.求证:AD=EB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{6}÷2=\sqrt{3}$ | C. | $\sqrt{2}$•$\sqrt{3}=\sqrt{6}$ | D. | $\sqrt{8}=4\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
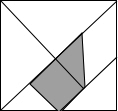 如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$.
如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com