
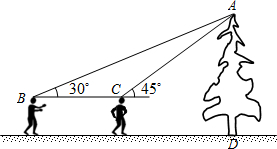
 某校初三学生去社会实践,在风景区看到一棵汉白杨树,好高哟,数学老师说请小明和小华同学用数学知识测量,全体同学计算这棵树多高,下面是这两位同学的对话.
某校初三学生去社会实践,在风景区看到一棵汉白杨树,好高哟,数学老师说请小明和小华同学用数学知识测量,全体同学计算这棵树多高,下面是这两位同学的对话.分析 延长BC交AD于E,设AE的长为x米,在Rt△ACE中,求得CE=AE,然后在Rt△ABE中求得BE,利用BE-CE=BC,可得关于x的方程,解得便求得结论.
解答 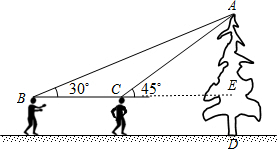 解:如图所示,延长BC交AD于E,
解:如图所示,延长BC交AD于E,
设AE的长为x米,由图可知,在Rt△ACE中,
∠ACE=45°,∠AEC=90°,则∠CAE=45°,∴EC=AE=x米,
在Rt△ABE中,∠B=30°,AE=x,
∴tanB=$\frac{AE}{BE}$,
即:tan30°=$\frac{x}{BE}$,
∴BE=$\sqrt{3}$x
∵BE-CE=BC,BC=20米,
∴$\sqrt{3}$x-x=20,
解得:x=10+10$\sqrt{3}$,
∴AD=10+10$\sqrt{3}$+1.6=28.9,
答:这棵古松的高是28.9米.
点评 本题考查了解直角三角形的应用,解题的关键是正确的利用直角三角形各边之间的关系得到有关未知量的关系式.


科目:初中数学 来源: 题型:选择题
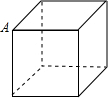 如图,A是正方体小木块(质地均匀)的顶点,将木块随机投掷在水平桌面上,则A与桌面接触的概率是( )
如图,A是正方体小木块(质地均匀)的顶点,将木块随机投掷在水平桌面上,则A与桌面接触的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 200名学生是总体 | |
| B. | 200名学生的体重是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 以上调查是普查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com