
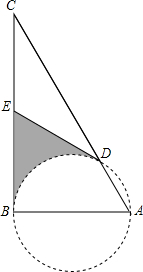
 如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.
如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.| 42-22 |
| 3 |
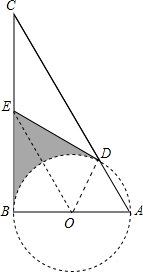 证明:(1)连接OD,OE,
证明:(1)连接OD,OE,
|
| 42-22 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 120π×22 |
| 360 |
12
| ||
| 3 |


科目:初中数学 来源: 题型:
 如图,轮船C在观测站A的北偏东60°方向,在观测站B的北偏西45°方向,则从轮船C看A、B两站的视角∠ACB=( )
如图,轮船C在观测站A的北偏东60°方向,在观测站B的北偏西45°方向,则从轮船C看A、B两站的视角∠ACB=( )| A、105° | B、100° |
| C、120° | D、110° |
查看答案和解析>>
科目:初中数学 来源: 题型:
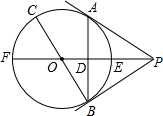 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F,过点A作PO的垂线AB,垂足为D,交⊙O于点B,BO的延长线交⊙O于点C.
如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F,过点A作PO的垂线AB,垂足为D,交⊙O于点B,BO的延长线交⊙O于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
 小明、小亮做一个“配色”的游戏.下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色.这种情况下小亮得1分;同样,蓝色和黄色在一起配成绿色,这种情况下小明得1分;在其它情况下,则小明、小亮不分胜负.这个游戏对双方公平吗?请说明理由.若不公平,如何修改游戏规则才能使游戏对双方公平?
小明、小亮做一个“配色”的游戏.下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色.这种情况下小亮得1分;同样,蓝色和黄色在一起配成绿色,这种情况下小明得1分;在其它情况下,则小明、小亮不分胜负.这个游戏对双方公平吗?请说明理由.若不公平,如何修改游戏规则才能使游戏对双方公平?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com