
如图,以矩形ABCD的对角线AC的中点O为圆心、OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K,过点D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。

(1)求证:AE=CK
(2)若AB=a,AD= a(a为常数),求BK的长(用含a的代数式表示)。
a(a为常数),求BK的长(用含a的代数式表示)。
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长。
(1)证明见解析;(2)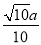 ;(3)
;(3)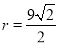 ,6.
,6.
【解析】
试题分析:(1)根据ABCD是矩形,求证△BKC≌△ADE即可;
(2)根据勾股定理求得AC的长,根据三角形的面积公式得出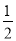 AB×BC=
AB×BC=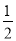 AC×BK,代入即可求得BK.
AC×BK,代入即可求得BK.
(3)根据三角形中位线定理可求出EF,再利用△AFD≌△HBF可求出HF,然后即可求出GH;利用射影定理求出AE,再利△AED∽△HEC求证AE=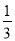 AC,然后即可求得AC即可.
AC,然后即可求得AC即可.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠DAE=∠BCK,
∵BK⊥AC,DH∥KB,
∴∠BKC=∠AED=90°,
∴△BKC≌△ADE,
∴AE=CK;
(2)【解析】
∵AB=a,AD= a=BC,
a=BC,
∴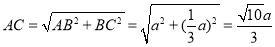
∵S△ABC=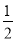 AB×BC=
AB×BC=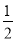 AC×BK,
AC×BK,
∴BK=
(3)连结OG,
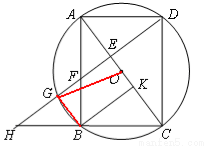
∵AC⊥DG,AC是⊙O的直径,DE=6,∴DE=EG=6,
又∵EF=FG,∴EF=3;
∵Rt△ADE≌Rt△CBK,∴DE=BK=6,AE=CK,
在△ABK中,EF=3,BK=6,EF∥BK,
∴EF是△ABK的中位线,
∴AF=BF,AE=EK=KC;
在Rt△OEG中,设OG=r,则OE=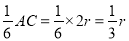 ,EG=6,
,EG=6, ,
,
∴ ,
,
∴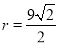 .
.
连接BG可得△BGF≌△AEF,AF=BF,△ADF≌△BHF
∵AD=BC,BF∥CD,∴HF=DF,
∵FG=EF,∴HF-FG=DF-EF,∴HG=DE=6.
考点:1.相似三角形的判定与性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.垂径定理.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:2014-2015学年辽宁省大石桥市八年级上学期段测数学试卷(解析版) 题型:选择题
如图,点D为△ABC边AB的中点,将△ABC沿经过点D的直线折叠,使点A刚好落在BC边上的点F处,若∠B=48°,则∠BDF的度数为( )
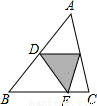
A.88° B.86° C.84° D.82°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷(解析版) 题型:填空题
如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=53°,则∠BOC的度数是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷(解析版) 题型:填空题
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=2n,则图中阴影部分的面积是( ).
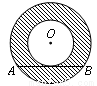
A.n2π B.2n2π C.4n2π D.8n2π
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市兴山县九年级上学期期末调研考试数学试卷(解析版) 题型:解答题
如图:在△ABC中,AD⊥BC,垂足是D.

(1)作△ABC的外接圆O,作直径AE(尺规作图);
(2)若AB=8,AC=6,AD=5,求△ABC的外接圆直径AE的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市兴山县九年级上学期期末调研考试数学试卷(解析版) 题型:选择题
下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省广水市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(6分)长岭中心中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全镇汉字听写大赛.
(1)请用树状图或列表法列举出各种可能选派的结果;
(2)求恰好选派一男一女两位同学参赛的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省商丘市九年级上学期期末考试数学试卷(解析版) 题型:选择题
△ABC与△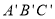 是位似图形,且△ABC与△
是位似图形,且△ABC与△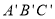 的位似比是1︰2,已知△ABC的面积是3,则△
的位似比是1︰2,已知△ABC的面积是3,则△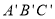 的面积是( )
的面积是( )
A.3 B.6 C.9 D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com