
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=2n,则图中阴影部分的面积是( ).
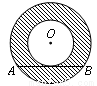
A.n2π B.2n2π C.4n2π D.8n2π
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年辽宁省大石桥市八年级上学期段测数学试卷(解析版) 题型:填空题
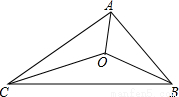
如图,已知△ABC的三边AB、AC、BC的长分别为20、30、40,其三条角平分线交于点O,则S△AOB:S△AOC:S△BOC= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷(解析版) 题型:解答题
如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于点E.

求:(1)CE的长;
(2)阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷(解析版) 题型:填空题
己知x1,x2是一元二次方x2-4x+1=0的两个根,则x1·x2= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市兴山县九年级上学期期末调研考试数学试卷(解析版) 题型:解答题
如图,以矩形ABCD的对角线AC的中点O为圆心、OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K,过点D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。

(1)求证:AE=CK
(2)若AB=a,AD= a(a为常数),求BK的长(用含a的代数式表示)。
a(a为常数),求BK的长(用含a的代数式表示)。
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省广水市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(12分)长岭中心中学九年级数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com