
【题目】在平面直角坐标系中,点A的坐标为(2,1),点B的坐标为(2,9),点C到直线AB的距离为4,且△ABC是直角三角形,则满足条件的点C有_____个.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
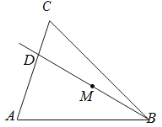
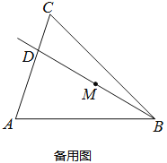
【题目】如图,在△ABC中,![]() ,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
(1)求线段BC的长;
(2)①当点D与点A、点C不重合时,过点D作DE⊥AB于点E,DF⊥BC于点F,连接ME,MF,在射线BD旋转的过程中,∠EMF的大小是否发生变化?若不变,求∠EMF的度数;若变化,请说明理由.
②在①的条件下,连接EF,直接写出△EFM面积的最小值______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解答后面的问题.
在学习了直角三角形的边角关系后,小颖和小明两个学习小组继续探究任意锐角三角形的边角关系:在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.
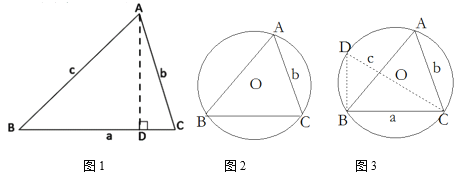
(1)小明学习小组发现如下结论:
如图1,过A作AD⊥BC于D,则sinB=![]() ,sinC=
,sinC=![]() 即AD=csinB,AD=bsinC,于是_____=______即
即AD=csinB,AD=bsinC,于是_____=______即![]() ,同理有
,同理有![]() ,
,![]()
则有![]()
(2)小颖学习小组则利用圆的有关性质也得到了类似的结论:
如图2,△ABC的外接圆半径为R,连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,
∵CD为⊙O的直径,∴∠DBC=90°,
在Rt△DBC中,
∵![]() ,
,
∴![]() ,
,![]()
同理:![]() ,
,
则有![]()
请你将这一结论用文字语言描述出来: .
小颖学习小组在证明过程中略去了“![]() ”的证明过程,请你把“
”的证明过程,请你把“![]() ”的证明过程补写出来.
”的证明过程补写出来.
(3)直接用前面阅读材料中得出的结论解决问题
规划局为了方便居民,计划在三个住宅小区A、B、C之间修建一座学校,使它到三个住宅小区的距离相等,已知小区C在小区B的正东方向![]() 千米处,小区A在小区B的东北方向,且A与C之间相距
千米处,小区A在小区B的东北方向,且A与C之间相距![]() 千米,求学校到三个小区的距离及小区A在小区C的什么方向?
千米,求学校到三个小区的距离及小区A在小区C的什么方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() .
.
(1)探索发现:

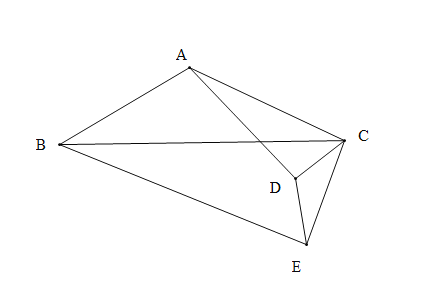
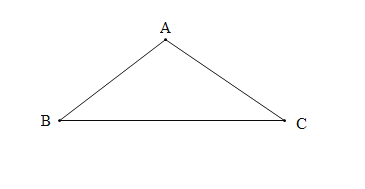
图1中,![]() 的值为_____________;
的值为_____________;![]() 的值为_________.
的值为_________.
(2)拓展探究
若将![]() 绕点
绕点![]() 逆时针方向旋转一周,在旋转过程中
逆时针方向旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当![]() 旋转至
旋转至![]() 三点在同一直线时,直接写出线段
三点在同一直线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物业公司计划对所管理的小区3000m2区域进行绿化,经投标由甲、乙两个工程队来完成,甲、乙两个工程队每天共完成绿化面积150m2,甲队完成600m2区域的绿化面积与乙队完成300m2区域的绿化面积所用的天数相同.
(1)求甲、乙两个工程队每天各能完成多少面积的绿化?
(2)若甲队每天绿化费用是0.6万元,乙队每天绿化费用是0.2万元,该物业公司要使这次绿化总费用不超过17万元,则至少安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格,每个小正方形的边长都为1,线段AB的端点落在格点上,要求画一个四边形,所作的四边形为中心对称图形,同时满足下列要求:
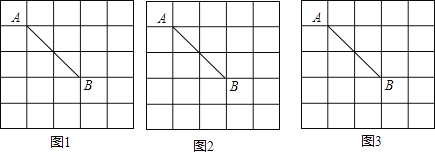
(1)在图1中画出以AB为一边的四边形;
(2)分别在图2和图3中各画出一个以AB为一条对角线的四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1的解析式为![]() ,直线l2的解析式为
,直线l2的解析式为![]() ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
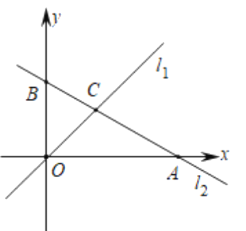

(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
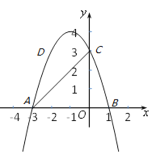
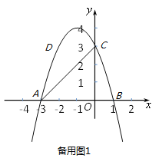
【题目】如图,抛物线与x轴相交于点A(-3,0)、点B(1,0),与y轴交于点C(0,3),点D是第二象限内抛物线上一动点.F点坐标为(-4,0).
(1)求这条抛物线的解析式;并写出顶点坐标;
(2)当D为抛物线的顶点时,求△ACD的面积;
(3)连接OD交线段AC于点E.当△AOE与△ABC相似时,求点D的坐标;
(4)在x轴上方作正方形AFMN,将正方形AFMN沿x轴下方向向右平移t个单位,其中0≤t≤4,设正方形AFMN与△ABC的重叠总分面积为S,直接写出S关于t的函数解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com