
°æƒø°ø‘ƒ∂¡œ¬¡–≤ƒ¡œ£¨≤¢Ω‚¥∫Û√ʵƒŒ £Æ
‘⁄—ßœ∞¡À÷±Ω«»˝Ω«–Œµƒ±flΩ«πÿœµ∫Û£¨–°”±∫Õ–°√˜¡Ω∏ˆ—ßœ∞–°◊ȺÖ¯ÃΩæø»Œ“‚»ÒΩ«»˝Ω«–Œµƒ±flΩ«πÿœµ£∫‘⁄»ÒΩ«°˜ABC÷–£¨°œA°¢°œB°¢°œCµƒ∂‘±fl∑÷± «a°¢b°¢c£Æ
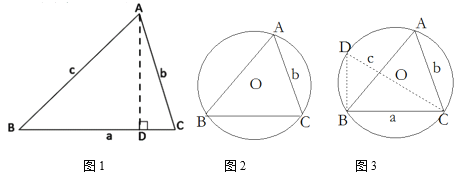
£®1£©–°√˜—ßœ∞–°◊È∑¢œ÷»Áœ¬Ω·¬€£∫
»ÁÕº1£¨π˝A◊˜AD°ÕBC”⁄D£¨‘ÚsinB=![]() £¨sinC=
£¨sinC=![]() º¥AD=csinB£¨AD=bsinC£¨”⁄ «_____=______º¥
º¥AD=csinB£¨AD=bsinC£¨”⁄ «_____=______º¥![]() £¨Õ¨¿Ì”–
£¨Õ¨¿Ì”–![]() £¨
£¨![]()
‘Ú”–![]()
£®2£©–°”±—ßœ∞–°◊È‘Ú¿˚”√‘≤µƒ”–πÿ–‘÷ “≤µ√µΩ¡À¿‡À∆µƒΩ·¬€£∫
»ÁÕº2£¨°˜ABCµƒÕ‚Ω”‘≤∞Îæ∂Œ™R£¨¡¨Ω·CO≤¢—”≥§Ωª°—O”⁄µ„D£¨¡¨Ω·DB£¨‘Ú°œD=°œA£¨
°flCDŒ™°—Oµƒ÷±æ∂£¨°‡°œDBC=90°„£¨
‘⁄Rt°˜DBC÷–£¨
°fl![]() £¨
£¨
°‡![]() £¨
£¨![]()
Õ¨¿Ì£∫![]() £¨
£¨
‘Ú”–![]()
«Îƒ„Ω´’‚“ªΩ·¬€”√Œƒ◊÷”Ô—‘√Ë ˆ≥ˆ¿¥: £Æ
–°”±—ßœ∞–°◊È‘⁄÷§√˜π˝≥Ã÷–¬‘»•¡À°∞![]() °±µƒ÷§√˜π˝≥㨫΃„∞—°∞
°±µƒ÷§√˜π˝≥㨫΃„∞—°∞![]() °±µƒ÷§√˜π˝≥Ã≤π–¥≥ˆ¿¥£Æ
°±µƒ÷§√˜π˝≥Ã≤π–¥≥ˆ¿¥£Æ
£®3£©÷±Ω””√«∞√Ê‘ƒ∂¡≤ƒ¡œ÷–µ√≥ˆµƒΩ·¬€Ω‚戌 Â
πʪÆæ÷Œ™¡À∑Ω±„æ”√Ò£¨º∆ªÆ‘⁄»˝∏ˆ◊°’¨–°«¯A°¢B°¢C÷ƺ‰–fiΩ®“ª◊˘—ß–££¨ πÀ¸µΩ»˝∏ˆ◊°’¨–°«¯µƒæ‡¿Îœ‡µ»£¨“—÷™–°«¯C‘⁄–°«¯Bµƒ’˝∂´∑ΩœÚ![]() «ß√◊¥¶£¨–°«¯A‘⁄–°«¯Bµƒ∂´±±∑ΩœÚ£¨«“A”ÎC÷ƺ‰œ‡æ‡
«ß√◊¥¶£¨–°«¯A‘⁄–°«¯Bµƒ∂´±±∑ΩœÚ£¨«“A”ÎC÷ƺ‰œ‡æ‡![]() «ß√◊£¨«Û—ß–£µΩ»˝∏ˆ–°«¯µƒæ‡¿Îº∞–°«¯A‘⁄–°«¯Cµƒ ≤√¥∑ΩœÚ£ø
«ß√◊£¨«Û—ß–£µΩ»˝∏ˆ–°«¯µƒæ‡¿Îº∞–°«¯A‘⁄–°«¯Cµƒ ≤√¥∑ΩœÚ£ø
°æ¥∞∏°ø£®1£©csinB£¨bsinC£ª£®2£©‘⁄»Œ“‚“ª∏ˆ»˝Ω«–Œ÷–£¨∏˜±fl∫ÕÀ¸À˘∂‘Ω«µƒ’˝œ“÷µµƒ±»œ‡µ»«“µ»”⁄Õ‚Ω”‘≤µƒ÷±æ∂£ª£®3£©—ß–£µΩ»˝∏ˆ–°«¯µƒæ‡¿ÎŒ™1«ß√◊£¨–°«¯A‘⁄–°«¯Cµƒ±±∆´Œ˜15°„µƒ∑ΩœÚ£Æ
°æΩ‚Œˆ°ø
£®1£©”…AD=csinB£¨AD=bsinCø…µ√¥∞∏£ª
£®2£©”…Ω·¬€ø…◊‹Ω·Œ™£∫‘⁄»Œ“‚“ª∏ˆ»˝Ω«–Œ÷–£¨∏˜±fl∫ÕÀ¸À˘∂‘Ω«µƒ’˝œ“÷µµƒ±»œ‡µ»«“µ»”⁄Õ‚Ω”‘≤µƒ÷±æ∂£¨æ›¥ÀΩ‚¥º¥ø…£ª
£®3£©∏˘æ›Ã‚“‚ª≠≥ˆÕº–Œ»ÁÕº£¨‘Ú°œB=45°„£¨BC=![]() «ß√◊£¨AC=
«ß√◊£¨AC=![]() «ß√◊£¨…Ë—ß–£µƒŒª÷√Œ™µ„O£¨‘ÚOA=OB=OC=R£¨”…‘ƒ∂¡≤ƒ¡œµƒΩ·¬€ø…µ√£∫
«ß√◊£¨…Ë—ß–£µƒŒª÷√Œ™µ„O£¨‘ÚOA=OB=OC=R£¨”…‘ƒ∂¡≤ƒ¡œµƒΩ·¬€ø…µ√£∫![]() £¨”…¥Àº¥ø…«Û≥ˆ°œBACµƒ∂» ˝∫ÕRµƒ÷µ£¨Ω¯∂¯ø…«Û≥ˆ°œACBµƒ∂» ˝£¨º¥µ√°œACNµƒ∂» ˝£¨Œ º¥µ√Ω‚æˆ£Æ
£¨”…¥Àº¥ø…«Û≥ˆ°œBACµƒ∂» ˝∫ÕRµƒ÷µ£¨Ω¯∂¯ø…«Û≥ˆ°œACBµƒ∂» ˝£¨º¥µ√°œACNµƒ∂» ˝£¨Œ º¥µ√Ω‚æˆ£Æ
Ω‚£∫£®1£©”…AD=csinB£¨AD=bsinCµ√£∫csinB=bsinC£ª
π ¥∞∏Œ™£∫csinB£¨bsinC£ª
£®2£©”…![]() ’‚“ªΩ·¬€”√Œƒ◊÷”Ô—‘√Ë ˆ≥ˆ¿¥ «£∫‘⁄»Œ“‚“ª∏ˆ»˝Ω«–Œ÷–£¨∏˜±fl∫ÕÀ¸À˘∂‘Ω«µƒ’˝œ“÷µµƒ±»œ‡µ»«“µ»”⁄Õ‚Ω”‘≤µƒ÷±æ∂£Æ
’‚“ªΩ·¬€”√Œƒ◊÷”Ô—‘√Ë ˆ≥ˆ¿¥ «£∫‘⁄»Œ“‚“ª∏ˆ»˝Ω«–Œ÷–£¨∏˜±fl∫ÕÀ¸À˘∂‘Ω«µƒ’˝œ“÷µµƒ±»œ‡µ»«“µ»”⁄Õ‚Ω”‘≤µƒ÷±æ∂£Æ
π ¥∞∏Œ™£∫‘⁄»Œ“‚“ª∏ˆ»˝Ω«–Œ÷–£¨∏˜±fl∫ÕÀ¸À˘∂‘Ω«µƒ’˝œ“÷µµƒ±»œ‡µ»«“µ»”⁄Õ‚Ω”‘≤µƒ÷±æ∂£ª
£®3£©»ÁÕº£¨”…“‚µ√£∫°œB=45°„£¨BC=![]() «ß√◊£¨AC=
«ß√◊£¨AC=![]() «ß√◊£¨…Ë—ß–£µƒŒª÷√Œ™µ„O£¨‘ÚOA=OB=OC=R£¨
«ß√◊£¨…Ë—ß–£µƒŒª÷√Œ™µ„O£¨‘ÚOA=OB=OC=R£¨
”…‘ƒ∂¡≤ƒ¡œµƒΩ·¬€ø…µ√£∫![]() £¨
£¨
º¥![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨![]() «ß√◊£¨
«ß√◊£¨
°‡°œBAC=60°„£¨
°‡°œACB=180°„£≠45°„£≠60°„=75°„£¨
°‡°œACN=15°„£¨º¥–°«¯A‘⁄–°«¯Cµƒ±±∆´Œ˜15°„µƒ∑ΩœÚ£Æ
¥£∫—ß–£µΩ»˝∏ˆ–°«¯µƒæ‡¿ÎŒ™1«ß√◊£¨–°«¯A‘⁄–°«¯Cµƒ±±∆´Œ˜15°„µƒ∑ΩœÚ£Æ



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂˛¥Œ∫Ø ˝![]() µƒ≤ø∑÷ÕºœÛ»ÁÕº£¨ÕºœÛπ˝µ„£®©Å1£¨0£©£¨∂‘≥∆÷·Œ™÷±œfl
µƒ≤ø∑÷ÕºœÛ»ÁÕº£¨ÕºœÛπ˝µ„£®©Å1£¨0£©£¨∂‘≥∆÷·Œ™÷±œfl![]() £¨œ¬¡–Ω·¬€£∫¢Ÿ
£¨œ¬¡–Ω·¬€£∫¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() £ª¢‹µ±
£ª¢‹µ±![]() ±£¨
±£¨ ![]() ÀÊ
ÀÊ![]() µƒ‘ˆ¥Û∂¯‘ˆ¥Û£Æ∆‰÷–’˝»∑µƒΩ·¬€”–£®°°°° £©
µƒ‘ˆ¥Û∂¯‘ˆ¥Û£Æ∆‰÷–’˝»∑µƒΩ·¬€”–£®°°°° £©

A. 1∏ˆ B. 2∏ˆ C. 3∏ˆ D. 4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
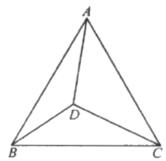
°æƒø°ø»ÁÕº£¨µ„![]() Œ™µ»±fl»˝Ω«–Œ
Œ™µ»±fl»˝Ω«–Œ![]() ƒ⁄“ªµ„£¨«“
ƒ⁄“ªµ„£¨«“![]() £¨‘Ú
£¨‘Ú![]() µƒ◊Ó–°÷µŒ™______£Æ
µƒ◊Ó–°÷µŒ™______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
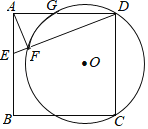
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒABCD÷–£¨EŒ™AB…œ“ªµ„£¨AF°ÕDE”⁄µ„F£¨“—÷™DF=5EF=5£¨π˝C°¢D°¢Fµƒ°—O”αflADΩª”⁄µ„G£¨‘ÚDG=(°°°°)
A.2![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
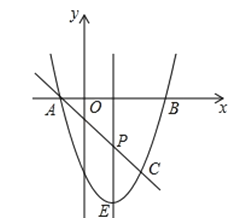
°æƒø°ø»ÁÕº£¨≈◊ŒÔœfly=ax2+bx©Å3”Îx÷·Ωª”⁄A£¨B¡Ωµ„£®Aµ„‘⁄Bµ„◊Û≤‡£©£¨A£®©Å1£¨0£©£¨B£®3£¨0£©£¨÷±œfll”Î≈◊ŒÔœflΩª”⁄A£¨C¡Ωµ„£¨∆‰÷–Cµ„µƒ∫·◊¯±ÍŒ™2£Æ
£®1£©«Û≈◊ŒÔœflµƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®2£©P «œfl∂ŒAC…œµƒ“ª∏ˆ∂ص„£¨π˝Pµ„◊˜y÷·µƒ∆Ω––œflΩª≈◊ŒÔœfl”⁄Eµ„£¨«Ûœfl∂ŒPE≥§∂»µƒ◊Ó¥Û÷µ£ª
£®3£©µ„G «≈◊ŒÔœfl…œµƒ∂ص„£¨‘⁄x÷·…œ «∑ҥʑ⁄µ„F£¨ πA£¨C£¨F£¨G’‚—˘µƒÀƒ∏ˆµ„Œ™∂•µ„µƒÀƒ±fl–Œ «∆Ω––Àƒ±fl–Œ£ø»Áπ˚¥Ê‘⁄£¨«Û≥ˆÀ˘”–¬˙◊„Ãıº˛µƒFµ„◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“√«÷™µ¿£¨”λ˝Ω«–Œ∏˜±fl∂ºœ‡«–µƒ‘≤Ω–◊ˆ»˝Ω«–Œµƒƒ⁄«–‘≤£¨‘Ú»˝Ω«–Œø…“‘≥∆Œ™‘≤µƒÕ‚«–»˝Ω«–Œ£Æ»ÁÕº1£¨![]() ”Î
”Î![]() µƒ»˝±fl
µƒ»˝±fl![]() ∑÷±œ‡«–”⁄µ„
∑÷±œ‡«–”⁄µ„![]() ‘Ú
‘Ú![]() Ω–◊ˆ
Ω–◊ˆ![]() µƒÕ‚«–»˝Ω«–Œ.“‘¥À¿‡Õ∆£¨∏˜±fl∂º∫Õ‘≤œ‡«–µƒÀƒ±fl–Œ≥∆Œ™‘≤Õ‚«–Àƒ±fl–Œ£Æ»ÁÕº2£¨
µƒÕ‚«–»˝Ω«–Œ.“‘¥À¿‡Õ∆£¨∏˜±fl∂º∫Õ‘≤œ‡«–µƒÀƒ±fl–Œ≥∆Œ™‘≤Õ‚«–Àƒ±fl–Œ£Æ»ÁÕº2£¨![]() ”ÎÀƒ±fl–ŒABCDµƒ±fl
”ÎÀƒ±fl–ŒABCDµƒ±fl![]() ∑÷±œ‡«–”⁄µ„
∑÷±œ‡«–”⁄µ„![]() ‘ÚÀƒ±fl–Œ
‘ÚÀƒ±fl–Œ![]() Ω–◊ˆ
Ω–◊ˆ![]() µƒÕ‚«–Àƒ±fl–Œ£Æ
µƒÕ‚«–Àƒ±fl–Œ£Æ
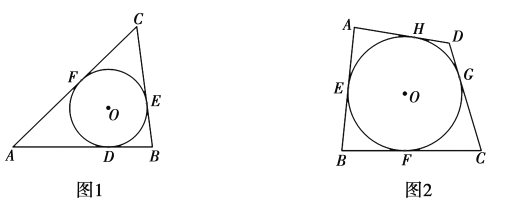
£®1£©»ÁÕº2£¨ ‘ÃΩæø‘≤Õ‚«–Àƒ±fl–Œ![]() µƒ¡Ω◊È∂‘±fl
µƒ¡Ω◊È∂‘±fl![]() ”Î
”Î![]() ÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¬œÎ£∫
÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¬œÎ£∫![]()
![]() (∫·œfl…œÃÓ°∞>°±£¨°∞<°±ªÚ°∞=°±)£ª
(∫·œfl…œÃÓ°∞>°±£¨°∞<°±ªÚ°∞=°±)£ª
£®2£©¿˚”√Õº2÷§√˜ƒ„µƒ≤¬œÎ(–¥≥ˆ“—÷™£¨«Û÷§£¨÷§√˜π˝≥Ã)£ª
£®3£©”√Œƒ◊÷– ˆ…œ√Ê÷§√˜µƒΩ·¬€£∫ £ª
£®4£©»Ù‘≤Õ‚«–Àƒ±fl–Œµƒ÷‹≥§Œ™![]() œ‡¡⁄µƒ»˝Ãı±flµƒ±»Œ™
œ‡¡⁄µƒ»˝Ãı±flµƒ±»Œ™![]() £¨«Û¥ÀÀƒ±fl–Œ∏˜±flµƒ≥§£Æ
£¨«Û¥ÀÀƒ±fl–Œ∏˜±flµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£Œ™œÏ”¶Œ“ –»´√Ò‘ƒ∂¡ªÓ∂Ø£¨¿˚”√Ω⁄ºŸ»’√ʜڅÁª·ø™∑≈—ß–£Õº Èπ›æ›Õ≥º∆£¨µ⁄“ª∏ˆ‘¬Ω¯π›128»À¥Œ£¨Ω¯π›»À¥Œ÷‘¬‘ˆº”£¨µΩµ⁄»˝∏ˆ‘¬ƒ©¿€º∆Ω¯π›608»À¥Œ£¨»ÙΩ¯π›»À¥Œµƒ‘¬∆Ωæ˘‘ˆ≥§¬ œ‡Õ¨£Æ
£®1£©«ÛΩ¯π›»À¥Œµƒ‘¬∆Ωæ˘‘ˆ≥§¬ £ª
£®2£©“ÚÃıº˛œfi÷∆£¨—ß–£Õº Èπ›√ø‘¬Ω”ƒ…ƒ‹¡¶≤ª≥¨π˝500»À¥Œ£¨‘⁄Ω¯π›»À¥Œµƒ‘¬∆Ωæ˘‘ˆ≥§¬ ≤ª±‰µƒÃıº˛œ¬£¨–£Õº È𛃋∑ÒΩ”ƒ…µ⁄Àƒ∏ˆ‘¬µƒΩ¯π›»À¥Œ£¨≤¢Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„Aµƒ◊¯±ÍŒ™£®2£¨1£©£¨µ„Bµƒ◊¯±ÍŒ™£®2£¨9£©£¨µ„CµΩ÷±œflABµƒæ‡¿ÎŒ™4£¨«“°˜ABC «÷±Ω«»˝Ω«–Œ£¨‘Ú¬˙◊„Ãıº˛µƒµ„C”–_____∏ˆ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨“—÷™æÿ–ŒABCD£¨AB=4£¨AD=3£¨µ„EŒ™±flDC…œ≤ª”Î∂Àµ„÷ÿ∫œµƒ“ª∏ˆ∂ص„£¨¡¨Ω”BE£¨Ω´BCE—ÿBE∑≠’€µ√µΩBEF£¨¡¨Ω”AF≤¢—”≥§ΩªCD”⁄µ„G£¨‘Úœfl∂ŒCGµƒ◊Ó¥Û÷µ «( )
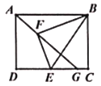
A.1B.1.5C.4-![]() D.4-
D.4-![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com