
【题目】我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1,![]() 与
与![]() 的三边
的三边![]() 分别相切于点
分别相切于点![]() 则
则![]() 叫做
叫做![]() 的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2,
的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2,![]() 与四边形ABCD的边
与四边形ABCD的边![]() 分别相切于点
分别相切于点![]() 则四边形
则四边形![]() 叫做
叫做![]() 的外切四边形.
的外切四边形.
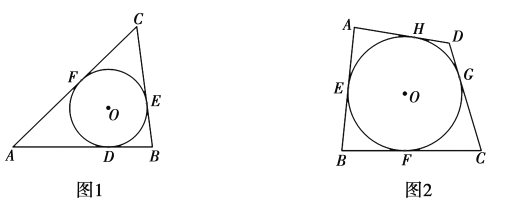
(1)如图2,试探究圆外切四边形![]() 的两组对边
的两组对边![]() 与
与![]() 之间的数量关系,猜想:
之间的数量关系,猜想:![]()
![]() (横线上填“>”,“<”或“=”);
(横线上填“>”,“<”或“=”);
(2)利用图2证明你的猜想(写出已知,求证,证明过程);
(3)用文字叙述上面证明的结论: ;
(4)若圆外切四边形的周长为![]() 相邻的三条边的比为
相邻的三条边的比为![]() ,求此四边形各边的长.
,求此四边形各边的长.
【答案】(1)=;(2)答案见解析;(3)圆外切四边形的对边之和相等;(4)4;10;12;6
【解析】
(1)根据圆外切四边形的定义猜想得出结论;
(2)根据切线长定理即可得出结论;
(3)由(2)可得出答案;
(4)根据圆外切四边形的性质求出第四边,利用周长建立方程求解即可得出结论.
解:(1)∵⊙O与四边形ABCD的边AB,BC,CD,DA分别相切于点E,F,G,H,
∴猜想AB+CD=AD+BC,
故答案为:=.
![]() 已知:四边形
已知:四边形![]() 的四边
的四边![]() 分别与
分别与![]() 相切于点
相切于点![]()
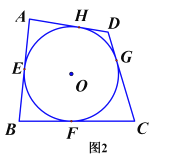
求证:![]()
证明:![]() 与
与![]() 相切,
相切,
![]()
同理:![]()
![]()
![]() 由(2)可知:圆外切四边形的对边和相等.
由(2)可知:圆外切四边形的对边和相等.
故答案为:圆外切四边形的对边和相等;
![]() 解:
解:![]() 相邻的三条边的比为
相邻的三条边的比为![]() ,
,
![]() 设此三边为
设此三边为![]()
根据圆外切四边形的性质得:第四边的长为:![]()
![]() 圆外切四边形的周长为
圆外切四边形的周长为![]() ,
,
![]()
解得![]()
![]() 此四边形的四边长分别为:
此四边形的四边长分别为:![]() .
.


科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
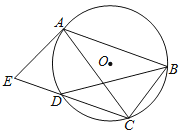
【题目】如图,四边形ABCD内接于⊙O,且AB=AC.延长CD至点E,使CE=BD,连接AE.
(1)求证:AD平分∠BDE;
(2)若AB//CD,求证:AE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
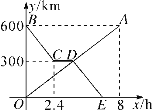
【题目】货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
(1)求点D的坐标,并解释点D的实际意义;
(2)求线段DE所在直线的函数表达式;
(3)当货车出发________h时,两车相距200km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解答后面的问题.
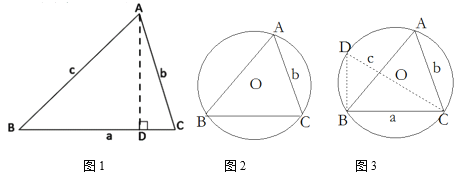
在学习了直角三角形的边角关系后,小颖和小明两个学习小组继续探究任意锐角三角形的边角关系:在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.
(1)小明学习小组发现如下结论:
如图1,过A作AD⊥BC于D,则sinB=![]() ,sinC=
,sinC=![]() 即AD=csinB,AD=bsinC,于是_____=______即
即AD=csinB,AD=bsinC,于是_____=______即![]() ,同理有
,同理有![]() ,
,![]()
则有![]()
(2)小颖学习小组则利用圆的有关性质也得到了类似的结论:
如图2,△ABC的外接圆半径为R,连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,
∵CD为⊙O的直径,∴∠DBC=90°,
在Rt△DBC中,
∵![]() ,
,
∴![]() ,
,![]()
同理:![]() ,
,
则有![]()
请你将这一结论用文字语言描述出来: .
小颖学习小组在证明过程中略去了“![]() ”的证明过程,请你把“
”的证明过程,请你把“![]() ”的证明过程补写出来.
”的证明过程补写出来.
(3)直接用前面阅读材料中得出的结论解决问题
规划局为了方便居民,计划在三个住宅小区A、B、C之间修建一座学校,使它到三个住宅小区的距离相等,已知小区C在小区B的正东方向![]() 千米处,小区A在小区B的东北方向,且A与C之间相距
千米处,小区A在小区B的东北方向,且A与C之间相距![]() 千米,求学校到三个小区的距离及小区A在小区C的什么方向?
千米,求学校到三个小区的距离及小区A在小区C的什么方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
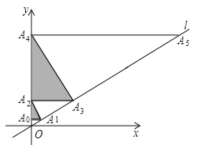
【题目】如图,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() …,这样依次下去,得到
…,这样依次下去,得到![]() ,…,其面积分别记为
,…,其面积分别记为![]() ,…,则
,…,则![]() 为__________.
为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() .
.
(1)探索发现:

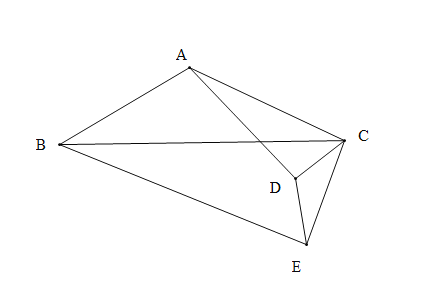
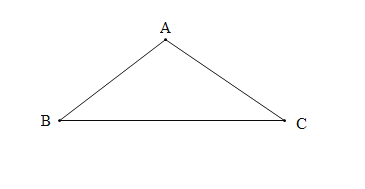
图1中,![]() 的值为_____________;
的值为_____________;![]() 的值为_________.
的值为_________.
(2)拓展探究
若将![]() 绕点
绕点![]() 逆时针方向旋转一周,在旋转过程中
逆时针方向旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当![]() 旋转至
旋转至![]() 三点在同一直线时,直接写出线段
三点在同一直线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格,每个小正方形的边长都为1,线段AB的端点落在格点上,要求画一个四边形,所作的四边形为中心对称图形,同时满足下列要求:
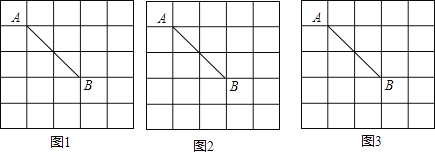
(1)在图1中画出以AB为一边的四边形;
(2)分别在图2和图3中各画出一个以AB为一条对角线的四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=-x2+(n-1)x+3的图像与y轴交于点A,与x轴的负半轴交于点B(-2,0)
(1)求二次函数的解析式;
(2)点P是这个二次函数图像在第二象限内的一线,过点P作y轴的垂线与线段AB交于点C,求线段PC长度的最大值.
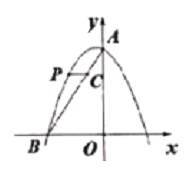
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com