
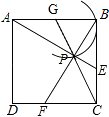
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个
【答案】D
【解析】解:如图,
∵动点F,E的速度相同,
∴DF=CE,
又∵CD=BC,
∴CF=BE,
在△ABE和△BCF中,

∴△ABE≌△BCF(SAS),故①正确;
∴∠BAE=∠CBF,AE=BF,故②正确;
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠APB=90°,故③正确;
在△BPE和△BCF中,
∵∠BPE=∠BCF,∠PBE=∠CBF,
∴△BPE∽△BCF,
∴ ![]() =
= ![]() ,
,
∴CFBE=PEBF,
∵CF=BE,
∴CF2=PEBF,故④正确;
∵点P在运动中保持∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
在Rt△BCG中,CG= ![]() =
= ![]() =
= ![]() ,
,
∵PG= ![]() AB=
AB= ![]() ,
,
∴CP=CG﹣PG= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
即线段CP的最小值为 ![]() ,故⑤正确;
,故⑤正确;
综上可知正确的有5个,
故选D.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】小明骑自行车上学,某天他从家出发骑行了一段路程,想起要买一本书,于是折回到他刚经过的某书店,买到书后继续去学校.以下是他在本次上学离家的距离与所用的时间的关系示意图,根据图中提供的信息解答下列问题:
(1)小明家与学校的距离是_____米.
(2)小明在书店停留了多少分钟?
(3)从A,B两题中任选一题作答:
A.小明骑行过程中哪个时间段的速度最快,最快的速度是多少?
B.小明在这次上学过程中的平均速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, ![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD, DE,直接写出△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对函数y=x+ ![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … | ﹣ | m | ﹣2 | ﹣ | ﹣ |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 , m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现: ①方程x+ ![]() =3有个实数根;
=3有个实数根;
②若关于x的方程x+ ![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 . 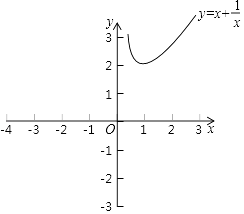
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”![]() 为了便于记忆,同学们可仿照图用双手表示“三线八角”
为了便于记忆,同学们可仿照图用双手表示“三线八角”![]() 两大拇指代表被截直线,食指代表截线
两大拇指代表被截直线,食指代表截线![]() 下列三幅图依次表示
下列三幅图依次表示![]()
![]()

A. 同位角、同旁内角、内错角B. 同位角、内错角、同旁内角
C. 同位角、对顶角、同旁内角D. 同位角、内错角、对顶角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论:
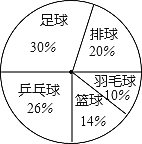
①最喜欢足球的人数最多,达到了15人;
②最喜欢羽毛球的人数最少,只有5人;
③最喜欢排球的人数比最喜欢乒乓球的人数少3人;
④最喜欢乒乓球的人数比最喜欢篮球的人数多6人。
其中正确的结论有
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com