
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB,BC分别交于点D,E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.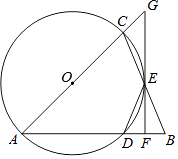
(1)求证:△BDE为等腰三角形;
(2)求证:GF⊥AB;
(3)若⊙O半径为3,DF=1,求CG的长.
【答案】
(1)证明:∵四边形ACED是⊙O的内接四边形,
∴∠ACB+∠ADE=180°,
∵∠BDE+∠ADE=180°,
∴∠BDE=∠ACB,
∵AB=AC,
∴∠B=∠ACB.
∴∠B=∠BDE,
∴△BDE为等腰三角形
(2)证明:连结OE,
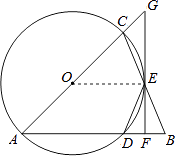
∵直线FG与⊙O相切,
∴∠OEG=90°,
∵OC=OE,
∴∠OEC=∠ACB,
∵∠B=∠ACB,
∴∠B=∠OEC,
∴OE∥AB,
∴∠AFG=∠OEG=90°,
即GF⊥AB
(3)解:设CG=x.
∵△BDE为等腰三角形,GF⊥AB,
∴BF=DF=1,AF=AB﹣BF=AC﹣BF=5,
∵OE∥AB,
∴△GOE∽△GAF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x= ![]() ,
,
即CG= ![]() .
.
【解析】(1)由四边形ACED是⊙O的内接四边形,得到∠ACB+∠ADE=180°,由于∠BDE+∠ADE=180°,得到∠BDE=∠ACB,即可得到结论;
(2)连结OE,根据切线的性质得到∠OEG=90°,根据等腰三角形的性质得到∠OEC=∠ACB,根据平行线的性质即可得到结论
(3)设CG=x.根据等腰三角形的性质得到BF=DF=1,AF=AB-BF=AC-BF=5,由相似三角形的判定和性质即可得到结论.
【考点精析】通过灵活运用等腰三角形的性质和圆内接四边形的性质,掌握等腰三角形的两个底角相等(简称:等边对等角);把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
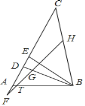
【题目】如图,在△ABC中,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②∠BEF=![]() (∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=
(∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=![]() (∠BAC﹣∠C);其中正确的是_____.
(∠BAC﹣∠C);其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是:______;
(3)画出△ABC中AB边上的中线CE;
(4)平移过程中,线段AC扫过的面积是_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )
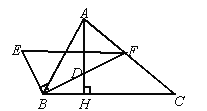
A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a﹣2b+c>0;④2c<3b;⑤当m≤x≤m+1时,函数的最大值为a+b+c,则0≤m≤1;
其中正确的结论有( )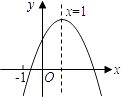
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】基本事实:“若ab=0,则a=0或b=0”.一元二次方程x2-x-2=0可通过因式分解化为(x-2)(x+1)=0,由基本事实得x-2=0或x+1=0,即方程的解为x=2或x=-1.
(1)、试利用上述基本事实,解方程:2x2-x=0:
(2)、若(x2+y2)(x2+y2-1)-2=0,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于未知数为 x,y 的二元一次方程组,如果方程组的解 x,y 满足![]() ,我们就说方程组的解 x 与 y 具有“邻好关系”.
,我们就说方程组的解 x 与 y 具有“邻好关系”.
(1) 方程组![]() 的解x与y是否具有“邻好关系”? 说明你的理由;
的解x与y是否具有“邻好关系”? 说明你的理由;
(2) 若方程组![]() 的解x与y具有“邻好关系”,求m的值;
的解x与y具有“邻好关系”,求m的值;
(3) 未知数为x,y的方程组![]() ,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com