
如图,在直角三角形ABC中,∠AC B=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
B=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
(1)CD的长;
(2)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(3)作出△BCD的边BC边上的高DF,当BD=11cm 时,求DF的长。
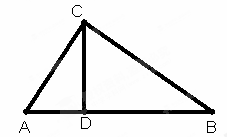
解:(1)在直角三角形ABC中,∠ACB=90° BC=12cm AC=5cm
∴△ABD的面积为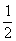 BC·AC=
BC·AC=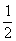 ×12×5=30cm2
×12×5=30cm2
∵CD是AB边上的高 AB=13cm
∴△ABD的面积又等于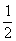 AB·CD=
AB·CD=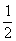 ×13CD=
×13CD=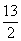 CD
CD
∴30=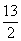 CD ∴CD=
CD ∴CD=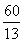 cm
cm
(2)作图略
∵BE是边AC的中线 AC=5cm ∴CE=2.5cm
∵∠ACB=90° ∴△BEC的面积=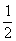 CE·BC=15cm2
CE·BC=15cm2
∴△ABE的面积=△ABC的面积-△BEC的面积
=30-15=15cm2
(3)作图略
∵DF是△A BC 的BC边上的高 CD是AB边上的高,
BC 的BC边上的高 CD是AB边上的高,
BD=11cm CD=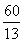 cm
cm
∴△CDB的面积=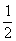 CD·BD=
CD·BD=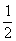 BC·DF
BC·DF
即
 ×11=
×11= ×12×DF
×12×DF
∴DF=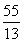 cm
cm


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源:2014-2015学年福建省永春县八年级上学期期末质量检测数学试卷(解析版) 题型:解答题
(8分)如图,在△ABC和△ABD中, AD=BC,∠DAB=∠CBA,
求证:AC=BD.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末监测数学试卷(解析版) 题型:选择题
下列说法错误的是( )
A.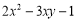 是二次三项式
是二次三项式
B. 不是单项式
不是单项式
C.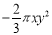 的系数是
的系数是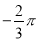
D. 的次数是6
的次数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象 是( )
是( )
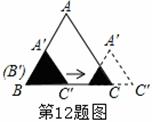

查看答案和解析>>
科目:初中数学 来源: 题型:
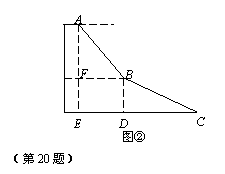
如图①,南京中山陵的台阶拾级而上被分成坡度不等的两部分.图②是台阶的侧面图,若斜坡BC长为120 m,在C处看B处的仰角为25°;斜坡AB长70 m,在A处看B处的俯角为50°,试求出陵墓的垂直高度AE的长.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47)
 | |||
| |||

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com