
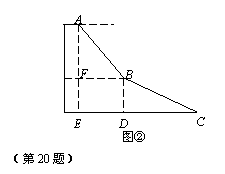
如图①,南京中山陵的台阶拾级而上被分成坡度不等的两部分.图②是台阶的侧面图,若斜坡BC长为120 m,在C处看B处的仰角为25°;斜坡AB长70 m,在A处看B处的俯角为50°,试求出陵墓的垂直高度AE的长.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47)
 | |||
| |||

解:在Rt△BDC中,sinC=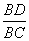 ,········································································· 1分
,········································································· 1分
∴BD=BC·sinC=BC·sin25°=120×0.42=50.4 m.··································· 3分
在Rt△AFB中,sin∠ABF= ,································································· 4分
,································································· 4分
∴AF=AB·sin∠ABF=AB·sin50°=70×0.77=53.9 m.····························· 6分
∴AE=AF+FE=AF+BD=50.4+53.9=104.3 m.
答:陵墓的垂直高度AE的长为104.3 m.······················································· 8分


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
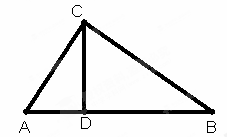
如图,在直角三角形ABC中,∠AC B=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
B=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
(1)CD的长;
(2)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(3)作出△BCD的边BC边上的高DF,当BD=11cm 时,求DF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
在正方形ABCD中,AD=2,l是过AD中点P的一条直线.O是l上一点,以O为圆心的圆经过点A、D,直线l与⊙O交于点E、F(E、F不与A、D重合,E在F的上面).
(1)如图,若点F在BC上,求证:BC与⊙O相切.并求出此时⊙O的半径.
(2)若⊙O半径为 ,请直接写出∠AED的度数.
,请直接写出∠AED的度数.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知四边形ABCD中.E、F分别是AB、AD边上的点,DE与CF交于点G。
(一)问题初探;
如图①,若四边形ABCD是正方形,且DE上CF.则DE与’CF的数量关系是
;
(二)类比延伸
(1)如图②若四边形ABCD是矩形.AB=m, AD=n.且DE⊥CF,则 = .(用含m,n的代数式表示)
= .(用含m,n的代数式表示)
(2)如图③,若四边形ABCD是平行四边形,当∠B+∠EGC=180°时,(1)中的结论是否成立,若成立,请证明你的结论;若不成立,请说明理由.
(三)拓展探究
如图④,若BA= BC= 6,DA= DC= 8,∠BAD= 90°.DE⊥CF,请直接写出 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com