考点:相交弦定理,垂径定理,射影定理
专题:证明题
分析:连CF,AC,AF,过A作AM⊥BF于M,由在同圆中等弧对的圆周角相等得到∠BCA=∠ACF,∠ACF=∠ABF,由同角的余角相等得到∠BAD=∠BCA,所以∠ABF=∠BAD,即BE=AE,证△AMB≌△BDA,推出AD=BM,求出BF=2AD,求出△ABE∽△FBA,推出AB2=BE×BF即可.
解答:证明:连CF,AC,AF,过A作AM⊥BF于M,
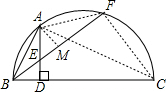
∵
=
,
∴AF=AB,∠BCA=∠ACF,∠ACF=∠ABF,
∴BF=2BM,
∵BC为圆的直径,∴∠BAC=90°,
∴∠ABC+∠ACB=90°,
又AD⊥BC,∴∠ADB=90°,
∴∠ABC+∠BAD=90°,
∴∠BAD=∠BCA,
∴∠ABF=∠BAD,
即BE=AE,
∵AM⊥BF,AD⊥BC,
∴∠AMB=∠ADB=90°,
在△AMB和△BDA中,
,
∴△AMB≌△BDA(AAS),
∴AD=BM,
∴BF=2AD,
∵弧AF=弧AB,
∴∠ABF=∠AFB,
∵∠ABF=∠BAD,
∴∠BAE=∠AFB,
∵∠ABE=∠ABE,
∴△ABE∽△FBA,
∴
=
,
∴AB
2=BE×BF,
∵BE=AE,BF=2AD,
∴AB
2=2AD×AE.
点评:本题考查了圆周角定理,相似三角形的性质和判定,全等三角形的性质和判定的应用,注意:在同圆中等弧对的圆周角相等,题目比较好,难度适中.

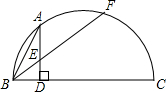 如图所示,BC是⊙O直径,AD⊥BC,垂足为D,
如图所示,BC是⊙O直径,AD⊥BC,垂足为D,






 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案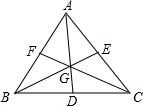 已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证:
已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证: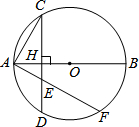 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为H.
如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为H.