Question

1．如图，已知平行四边形ABCD，AD⊥BD，AD=$2\sqrt{5}$，BD=2AD，过D点作DE⊥AB于E，以DE为直角边作等腰直角三角形DEF，点F落在DC上，将△DEF在同一平面内沿直线DC翻折，所得的等腰直角三角形记为△PQR，点R与D重合，点Q与F重合，如图①，平行四边形ABCD保持不动，将△PQR沿折线D-B-C匀速平移，点R的移动的速度为每秒$\sqrt{5}$个单位，设运动时间为t，当R与C重合时停止运动．
（1）当点Q落在BC边上时，求t的值；
（2）记△PQR与△DBC的重叠部分的面积为S，直接写出S与t之间的函数关系式，并写出相应的t的取值范围；
（3）当△PQR移动到R与B重合时，如图②，再将△PQR绕R点沿顺时针方向旋转α（0°≤α≤360°），得到△P₁Q₁R，若直线P₁Q₁与直线BC、直线DC分别相交于M、N，问在旋转的过程中是否存在△CMN为直角三角形，若存在，求出CN的长；若不存在，请说明理由．

Answer 1

分析 （1）根据同角的三角函数设未知数，利用勾股定理求AE、DE的长度，由翻折和平移的性质得到PD=DF=4，PR=RQ=4，利用勾股定理求BR的长，从而得到RD的长，根据速度为$\sqrt{5}$求出t；
（2）分四种情况分类讨论，①当0＜t≤$\frac{12}{5}$时，如图2，重叠部分是四边形GRQH，根据面积公式求梯形GRQH的面积就是S；②当$\frac{12}{5}$＜t≤4时，如图3，重叠部分是五边形GRNMH，S=S_△PRQ-S_△PGH-S_△MNQ，代入面积公式计算即可；③如图4，先计算当PQ经过点C时t=$\frac{14}{3}$，当4＜t≤$\frac{14}{3}$时，如图5，重叠部分为四边形GRMH，根据S=S_△PRQ-S_△PGH-S_△RMQ，代入求出；④当$\frac{14}{3}$＜t≤6时，如图6，重叠部分为三角形GRC，代入面积公式计算即可；
（3）根据旋转的度数，分三种情况讨论：①如图7，∠CNM=90°，CN=PN-PC=2$\sqrt{2}$-2；②如图8，∠CMN=90°，利用余弦求CN的长；③如图9，∠CNM=90°，CN=PC+PN=2+2$\sqrt{2}$．

解答 解：（1）如图1，当点Q落在BC边上时，点R运动的路程就等于RD的长，
∵AD⊥BD，DE⊥AB，
∴∠ADB=∠DEA=90°，
∴tan∠DAB=$\frac{BD}{AD}=\frac{ED}{AE}$，
∵BD=2AD，
∴$\frac{ED}{AE}$=2，
设AE=x，则ED=2x，
由勾股定理得：x²+（2x）²=（2$\sqrt{5}$）²，
5x²=20，
x₁=2，x₂=-2（舍），
∴AE=2，DE=4，
∵△DEF是等腰直角三角形，
∴DE=DF=4，
由翻折得：PD=DF=4，PR=RQ=4，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DBC=∠ADB=90°，
由平移得：RQ∥DC，
∴∠BRQ=∠BDC，
∴tan∠BRQ=tan∠BDC，
∴$\frac{BC}{BD}=\frac{BQ}{BR}$=$\frac{2\sqrt{5}}{4\sqrt{5}}$=$\frac{1}{2}$，
设BQ=x，则BR=2x，
由勾股定理得：x²+（2x）²=4²，
解得：x₁=$\frac{4\sqrt{5}}{5}$，x₂=-$\frac{4\sqrt{5}}{5}$（舍），
∴BR=2x=$\frac{8\sqrt{5}}{5}$，
∴RD=BD-BR=4$\sqrt{5}$-$\frac{8\sqrt{5}}{5}$=$\frac{12\sqrt{5}}{5}$，
∴t=$\frac{\frac{12\sqrt{5}}{5}}{\sqrt{5}}$=$\frac{12}{5}$；
（2）分四种情况：
由勾股定理得：DC=AB=$\sqrt{（4\sqrt{5}）^{2}+（2\sqrt{5}）^{2}}$=10，
①当0≤t≤$\frac{12}{5}$时，如图2，重叠部分是四边形GRQH，
则DR=$\sqrt{5}$t，
在Rt△DGR中，tan∠CDB=$\frac{RG}{DG}=\frac{1}{2}$，
设RG=x，则DG=2x，
∴x²+（2x）²=（$\sqrt{5}$t）²，
解得：x=±t，
∴RG=t，
∴GH=PG=4-t，
∴S=S_梯形GRQH=$\frac{1}{2}$（GH+RQ）•GR=$\frac{1}{2}$（4-t+4）•t=-$\frac{1}{2}{t}^{2}$+4t；
②当$\frac{12}{5}$＜t≤4时，如图3，重叠部分是五边形GRNMH，
同理得：GR=t，PG=GH=4-t，DR=$\sqrt{5}$t，
∴RB=4$\sqrt{5}$-$\sqrt{5}$t，
∴BN=$\frac{4\sqrt{5}-\sqrt{5}t}{2}$，
∵RN∥DC，
∴$\frac{RN}{DC}=\frac{BR}{BD}$，
∴$\frac{RN}{10}=\frac{\frac{4\sqrt{5}-\sqrt{5}t}{2}}{4\sqrt{5}}$，
∴RN=5-$\frac{5}{4}$t，
∴NQ=4-RN=4-5+$\frac{5}{4}$t=$\frac{5}{4}$t-1，
过M作MT⊥RQ于T，
tan∠MNQ=tan∠RNB=$\frac{MT}{NT}=\frac{RB}{BN}$=2，
∴MT=2NT，
∵∠Q=45°，∠MTQ=90°，
∴MT=TQ，
∴NT=$\frac{1}{3}$NQ=$\frac{1}{3}$（$\frac{5}{4}$t-1）=$\frac{5}{12}$t-$\frac{1}{3}$，
∴MT=2NT=$\frac{5}{6}$t-$\frac{2}{3}$，
∴S=S_△PRQ-S_△PGH-S_△MNQ，
=$\frac{1}{2}$×4×4-$\frac{1}{2}$（4-t）²-$\frac{1}{2}$（$\frac{5}{4}$t-1）（$\frac{5}{6}$t+$\frac{2}{3}$），
=-$\frac{49}{48}$t²+$\frac{29}{6}$t-$\frac{1}{3}$；
③如图4，当PQ经过点C时，过C作CN⊥PQ于N，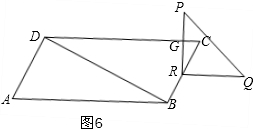
同理得：RN=$\frac{4}{3}$，NQ=CN=$\frac{8}{3}$，
∴RC=$\sqrt{（\frac{8}{3}）^{2}+（\frac{4}{3}）^{2}}$=$\frac{4\sqrt{5}}{3}$，
∴BD+BR=BD+BC-RC=4$\sqrt{5}$+2$\sqrt{5}$-$\frac{4\sqrt{5}}{3}$=$\frac{14}{3}$$\sqrt{5}$，
这时t=$\frac{14\sqrt{5}}{3}$÷$\sqrt{5}$=$\frac{14}{3}$；
当4＜t≤$\frac{14}{3}$时，如图4，重叠部分为四边形GRMH，
∵BD+BR=$\sqrt{5}$t，
∴BR=$\sqrt{5}$t-4$\sqrt{5}$，RC=6$\sqrt{5}$-$\sqrt{5}$t，
cos∠GRC=$\frac{RG}{RC}$=$\frac{4\sqrt{5}}{10}$，
∴$\frac{RG}{6\sqrt{5}-\sqrt{5}t}$=$\frac{4\sqrt{5}}{10}$，
∴RG=12-2t，
∴PG=4-（12-2t）=2t-8，
∴S=S_△PRQ-S_△PGH-S_△RMQ，
=$\frac{1}{2}$×4×4-$\frac{1}{2}$×（2t-8）²-$\frac{1}{2}$×4×$\frac{8}{3}$，
=-2t²+16t-$\frac{88}{3}$；
④当$\frac{14}{3}$＜t≤6时，如图6，重叠部分为三角形GRC，
由③得RG=12-2t，则CG=6-t，
∴S=S_△GRC=$\frac{1}{2}$CG•RG=$\frac{1}{2}$（12-2t）（6-t）=t²-12t+36；
综上所述：S=$\left\{\begin{array}{l}{-\frac{1}{2}{t}^{2}+4（0≤t≤\frac{12}{5}）}\\{-\frac{49}{48}{t}^{2}+\frac{29}{6}t-\frac{1}{3}（\frac{12}{5}＜t≤4）}\\{-2{t}^{2}+16t-\frac{88}{3}（4＜t≤\frac{14}{3}）}\\{{t}^{2}-12t+36（\frac{14}{3}＜t≤6）}\end{array}\right.$
（3）存在，分三种情况：
①如图7，∠CNM=90°，
∵DN∥AG，
∴∠AGM=∠CNM=90°，
∴△BGP₁是等腰直角三角形，
∴BG=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$，
由（1）得：CP=2，
∵PN=BG=2$\sqrt{2}$，
∴CN=PN-PC=2$\sqrt{2}$-2；
②如图8，∠CMN=90°，
∵BC=2$\sqrt{5}$，BM=2$\sqrt{2}$，
∴CM=2$\sqrt{2}$+2$\sqrt{5}$，
cos∠NCM=$\frac{PC}{BC}=\frac{CM}{CN}$，
∴$\frac{2}{2\sqrt{5}}$=$\frac{2\sqrt{2}+2\sqrt{5}}{CN}$，
∴CN=$\sqrt{5}$（2$\sqrt{2}$+2$\sqrt{5}$）=2$\sqrt{10}$+10；
③如图9，∠CNM=90°，
∵PN=BG=2$\sqrt{2}$，PC=2，
∴CN=PC+PN=2+2$\sqrt{2}$；
综上所述：CN的长为2$\sqrt{2}$-2或2$\sqrt{10}$+10或2+2$\sqrt{2}$．

点评 本题是几何变换的综合题，考查了平行四边形、等腰直角三角形的性质；同时还运用了同角的三角函数列比例式求边的长，比利用三角形相似列比例式要简单；在求重叠部分图形的面积时，先确定特殊位置时的t值，根据重叠图形分类讨论解决，利用面积差或和求解．