
【题目】已知:如图,平行四边形 ABCD的两条对角线相交于点O, E是BO的中点.过B点作AC的平行线,交CE的延长线于点F,连接BF.
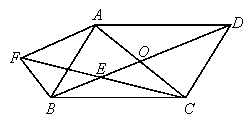
(1)求证:FB=AO;
(2)当平行四边形 ABCD满足什么条件时,四边形AFBO是菱形?说明理由.
【答案】(1)证明见解析;(2)当平行四边形ABCD是矩形时,四边形AFBO是菱形.理由见解析.
【解析】
试题分析:(1)如图,取BC的中点G.由三角形中位线定理易证EG=![]() BF=
BF=![]() OC;则由“有一组对边平行且相等的四边形为平行四边形”证得四边形AOBF为平行四边形.所以平行四边形的对边相等:FB=AO;
OC;则由“有一组对边平行且相等的四边形为平行四边形”证得四边形AOBF为平行四边形.所以平行四边形的对边相等:FB=AO;
(2)若四边形AFBO是菱形,则OB=OA.故当平行四边形ABCD的对角线相等,即平行四边形ABCD是矩形时,四边形AFBO是菱形.
试题解析:(1)如图,取BC的中点G,连接EG.

∵E是BO的中点,
∴EG是△BFC的中位线,
∴EG=![]() BF.
BF.
同理,EG=![]() OC,
OC,
∴BF=OC.
又∵点O是ABCD的对角线交点,
∴AO=CO,
∴BF=AO.
又∵BF∥AC,即BF∥AO,
∴四边形AOBF为平行四边形,
∴FB=AO;
(2)当平行四边形ABCD是矩形时,四边形AFBO是菱形.理由如下:
∵平行四边形ABCD是矩形,
∴OA=OB,
∴平行四边形AFBO是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
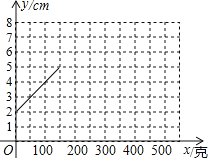
【题目】弹簧是一种利用弹性来工作的机械零件,用弹性材料制成的零件在外力作用下发生形变,除去外力后又恢复原状.某班同学在探究弹簧的长度与所受外力的变化关系时,通过实验记录得到的数据如下表:
砝码的质量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
指针的位置y(cm) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究,下面是小腾的探究过程,请补充完整.
(1)根据上述表格在平面直角坐标系中补全该函数的图象;
(2)根据画出的函数图象,写出:
①当x=0时,y= ,它的实际意义是 ;
②当指针的位置y不变时,砝码的质量x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
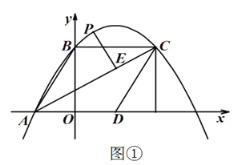
【题目】如图①,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,将
两点,将![]() 沿
沿![]() 轴正方向平移后,点
轴正方向平移后,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,且四边形
,且四边形![]() 为菱形,连接
为菱形,连接![]() ,抛物线
,抛物线![]() 经过
经过![]() 三点,点
三点,点![]() 为
为![]() 上方抛物线上一动点,作
上方抛物线上一动点,作![]() ,垂足为
,垂足为![]()
![]() 求此抛物线的函数关系式;
求此抛物线的函数关系式;
![]() 求线段
求线段![]() 长度的最大值;
长度的最大值;
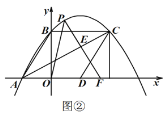
![]() 如图②,延长
如图②,延长![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,若
,若![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
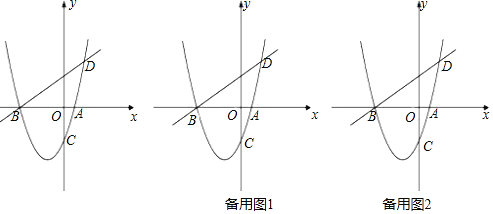
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且
与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C,求![]() 面积的最大值;
面积的最大值;
(3)在(2)中![]() 面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师每天要骑车到离家15千米的单位上班,若将速度提高原来的![]() ,则时间可缩短15分钟.
,则时间可缩短15分钟.
(1)求李老师原来的速度为多少千米/时;
(2)李老师按照原来的速度骑车到途中的A地,发现公文包忘在家里,他立即提速1倍回到家里取公文包(其他时间忽略不计),并且以返回时的速度赶往单位,若李老师到单位的时间不超过平时到校的时间,求A地距家最多多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
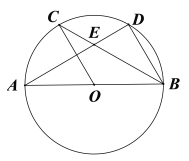
(1)求证:![]() ;
;
(2)若CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在直角坐标系中,平行四边形OABC的顶点A,C坐标分别为A(2,0),C(-1,2),反比例函数![]() 的图象经过点B (m≠0)
的图象经过点B (m≠0)
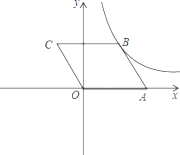
(1)求出反比例函数的解析式
(2)将![]() OABC沿着x轴翻折,点C落在点D处,做出点D并判断点D是否在反比例函数
OABC沿着x轴翻折,点C落在点D处,做出点D并判断点D是否在反比例函数![]() 的图象上
的图象上
(3)在x轴是否存在一点P使△OCP为等腰三角形,若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与函数
与函数![]()
![]() 的图象交于点
的图象交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与函数
,与函数![]()
![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①若点![]() 是线段
是线段![]() 的中点时,则点
的中点时,则点![]() 的坐标是______,
的坐标是______,![]() 的值是______;(直接写答案)
的值是______;(直接写答案)
②当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
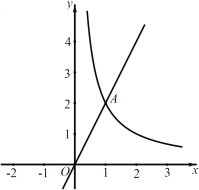
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com