
【题目】如图,△ABC中以AB为直径作⊙O,分别交边AC、BC于D、E,过D作DF⊥BC于F,且D为弧AE的中点.
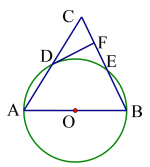
(1)求证:DF为⊙O的切线;
(2)若![]() 且AD=
且AD=![]() 时,求⊙O的半径
时,求⊙O的半径![]() .
.
【答案】(1)见解析;(2)r=10
【解析】
(1)如图,作辅助线;证明AE∥DF;利用垂径定理的推论证明OD⊥AE,即可解决问题.
(2)连接AE交OD于H,根据圆周角的性质求得AE⊥BE,根据垂径定理求得OD⊥AE,从而求得OD∥BC,进而求得OH=![]() BE,根据题意设BE=3x,则AB=5x,由勾股定理得,AE=4x,进而得出AH=2x,OH=1.5x,DH=x,然后根据勾股定理求得AD=
BE,根据题意设BE=3x,则AB=5x,由勾股定理得,AE=4x,进而得出AH=2x,OH=1.5x,DH=x,然后根据勾股定理求得AD=![]() x,又因为AD=4
x,又因为AD=4![]() ,即可求得x=4,进而求得⊙O的半径.
,即可求得x=4,进而求得⊙O的半径.
证明:(1)如图,连接AE、OD;
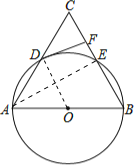
∵AB为⊙O的直径,
∴AE⊥BC,而DF⊥BC,
∴AE∥DF;
∵D为弧AE的中点
∴OD⊥AE,
∴OD⊥DF,
即DF为⊙O的切线.
(2)连接AE交OD于H,
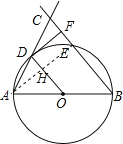
∵AB是⊙O的直径,
∴∠AEB=90°,
即AE⊥BE,
∵D为弧AE的中点,
∴OD⊥AE,
∴OD∥BC,
∵OA=OB,
∴OH=![]() BE,
BE,
在RT△ABE中,![]()
,设BE=3x,则AB=5x,由勾股定理得,AE=4x,
∴AH=2x,OH=1.5x,
∴DH=OD-OH=2.5x-1.5x=x,
在RT△ADH中,AD=![]()
∵AD=4![]() ,
,
∴x=4,
∴⊙O的半径=4×2.5=10.


科目:初中数学 来源: 题型:
【题目】如图1,两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
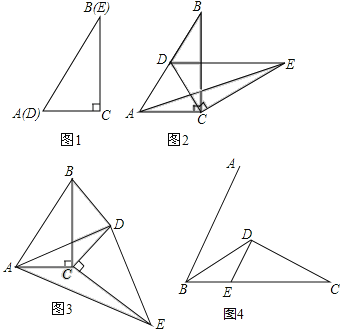
(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是 ;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 .
(2)猜想论证
当△DEC绕点C旋转到如图3所示的位置时,请猜想(1)中S1与S2的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)拓展探究
已知∠ABC=60°,BD平分∠ABC,BD=CD,BC=9,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请求相应的BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
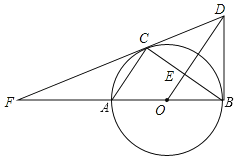
【题目】如图,已知AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.
(1)求证:DC是⊙O的切线;
(2)若∠ABC=30°,AB=8,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,
(1)该二次函数图象与x轴的交点坐标是______________;
(2)将![]() 化成
化成![]() 的形式_____________________,并写出顶点坐标______________.
的形式_____________________,并写出顶点坐标______________.
(3)在坐标轴中画出此抛物线的大致图象;
(4)写出不等式![]() 的解集___________________;
的解集___________________;
(5)当![]() 时,直接写出y的取值范围_________________.
时,直接写出y的取值范围_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
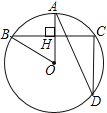
(1)若∠AOB=50°,求∠ADC的度数;
(2)若BC=8,AH=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司规定:一名客户如果一个月的通话时间不超过![]() 分钟,那么这个月这名客户只要交10元通话费;如果超过
分钟,那么这个月这名客户只要交10元通话费;如果超过![]() 分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟
分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟![]() 元交费.
元交费.
(Ⅰ)某名客户7月份通话90分钟,超过了规定的![]() 分钟,则超过部分应交通话费______元(用含
分钟,则超过部分应交通话费______元(用含![]() 的代数式表示);
的代数式表示);
(Ⅱ)下表表示某名客户8月份、9月份的通话情况和交费情况:
月份 | 通话时间/分钟 | 通话费总数/元 |
8月份 | 80 | 25 |
9月份 | 45 | 10 |
根据上表的数据,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程
的方程![]() .
.
(1)求证:无论![]() 取何值,这个方程总有实数根.
取何值,这个方程总有实数根.
(2)若方程的两根都是正数,求![]() 的取值范围.
的取值范围.
(3)以方程的两根为![]() 两边,斜边为
两边,斜边为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛,射击队对两人的射击技能进行了测评.在相同的条件下,两人各打靶5次,成绩统计如下:
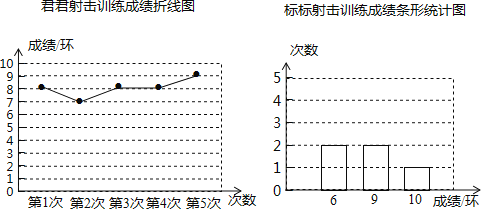
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
(2)根据以上信息,若选派一名队员参赛,你认为应选哪名队员,并说明理由.
(3)如果标标再射击1次,命中8环,那么他射击成绩的方差会 .(填“变大”“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
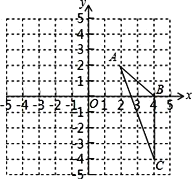
【题目】如图,在平面直角坐标系中,△ABC三个顶点分别是A(2,2),B(4,0),C(4,﹣4)
(1)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2
,得到△A2B2C2,请在y轴右侧画出△A2B2C2
(2)求出∠A2C2B2的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com