
【题目】已知关于![]() 的方程
的方程![]() .
.
(1)求证:无论![]() 取何值,这个方程总有实数根.
取何值,这个方程总有实数根.
(2)若方程的两根都是正数,求![]() 的取值范围.
的取值范围.
(3)以方程的两根为![]() 两边,斜边为
两边,斜边为![]() ,求
,求![]() 的值.
的值.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
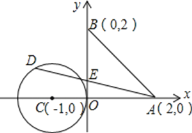
【题目】如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E ,则△ABE面积的最小值是 _____
查看答案和解析>>
科目:初中数学 来源: 题型:
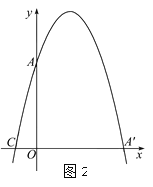
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中以AB为直径作⊙O,分别交边AC、BC于D、E,过D作DF⊥BC于F,且D为弧AE的中点.
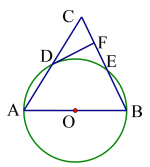
(1)求证:DF为⊙O的切线;
(2)若![]() 且AD=
且AD=![]() 时,求⊙O的半径
时,求⊙O的半径![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若抛物线![]() 与抛物线
与抛物线![]() 的开口大小相同,方向相反,且抛物线
的开口大小相同,方向相反,且抛物线![]() 经过
经过![]() 的顶点,我们称抛物线
的顶点,我们称抛物线![]() 为
为![]() 的“友好抛物线”.
的“友好抛物线”.
(1)若![]() 的表达式为
的表达式为![]() ,求
,求![]() 的“友好抛物线”的表达式;
的“友好抛物线”的表达式;
(2)已知抛物线![]() 为
为![]() 的“友好抛物线”.求证:抛物线
的“友好抛物线”.求证:抛物线![]() 也是
也是![]() 的“友好抛物线”;
的“友好抛物线”;
(3)平面上有点![]() ,
,![]() ,抛物线
,抛物线![]() 为
为![]() 的“友好抛物线”,且抛物线
的“友好抛物线”,且抛物线![]() 的顶点在第一象限,纵坐标为2,当抛物线
的顶点在第一象限,纵坐标为2,当抛物线![]() 与线段
与线段![]() 没有公共点时,求
没有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
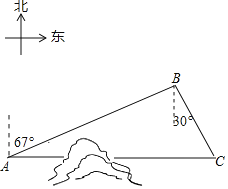
【题目】如图,C地在A地的正东方向,因有大山阻隔.由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地130km,C地位于B地南偏东30°方向.若打通穿山隧道.建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.
的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.

(1)请直接写出二次函数![]() 的解析式.
的解析式.
(2)判断△ABC的形状,并说明理由.
(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解: ![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
根据你的观察,探究下面的问题:
(1)己知![]() ,求
,求![]() 的值.
的值.
(2)已知△ABC的三边长a、b、c都是正整数,且满足![]() ,求边c的最大值.
,求边c的最大值.
(3) 若己知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com