
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解: ![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
根据你的观察,探究下面的问题:
(1)己知![]() ,求
,求![]() 的值.
的值.
(2)已知△ABC的三边长a、b、c都是正整数,且满足![]() ,求边c的最大值.
,求边c的最大值.
(3) 若己知![]() ,求
,求![]() 的值.
的值.
【答案】(1)2(2)6(3)7
【解析】分析:(1)将多项式第三项分项后,结合并利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出x与y的值,即可求出x﹣y的值;
(2)将已知等式25分为9+16,重新结合后,利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出a与b的值,根据边长为正整数且三角形三边关系即可求出c的长;
(3)由a﹣b=4,得到a=b+4,代入已知的等式中重新结合后,利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出b与c的值,进而求出a的值,即可求出a﹣b+c的值.
详解:(1)∵x2+2xy+2y2+2y+1=0
∴(x2+2xy+y2)+(y2+2y+1)=0
∴(x+y)2+(y+1)2=0
∴x+y=0 y+1=0
解得:x=1,y=﹣1
∴x﹣y=2;
(2)∵a2+b2﹣6a﹣8b+25=0
∴(a2﹣6a+9)+(b2﹣8b+16)=0
∴(a﹣3)2+(b﹣4)2=0
∴a﹣3=0,b﹣4=0
解得:a=3,b=4
∵三角形两边之和>第三边
∴c<a+b,c<3+4,∴c<7.又∵c是正整数,∴△ABC的最大边c的值为4,5,6,∴c的最大值为6;
(3)∵a﹣b=4,即a=b+4,代入得:(b+4)b+c2﹣6c+13=0,整理得:(b2+4b+4)+(c2﹣6c+9)=(b+2)2+(c﹣3)2=0,∴b+2=0,且c﹣3=0,即b=﹣2,c=3,a=2,则a﹣b+c=2﹣(﹣2)+3=7.
故答案为:7.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程
的方程![]() .
.
(1)求证:无论![]() 取何值,这个方程总有实数根.
取何值,这个方程总有实数根.
(2)若方程的两根都是正数,求![]() 的取值范围.
的取值范围.
(3)以方程的两根为![]() 两边,斜边为
两边,斜边为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的衍生点.
(1)若方程为x2-2x=0,写出该方程的衍生点M的坐标.
(2)若关于x的一元二次方程x2-(2m+1)x+2m=0(m<0)的衍生点为M,过点M向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.
(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M始终在直线y=kx-2(k-2)的图象上,若有请直接写出b,c的值,若没有说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
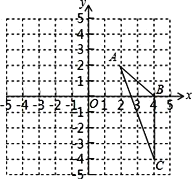
【题目】如图,在平面直角坐标系中,△ABC三个顶点分别是A(2,2),B(4,0),C(4,﹣4)
(1)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2
,得到△A2B2C2,请在y轴右侧画出△A2B2C2
(2)求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为( )米.
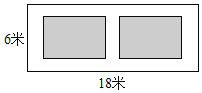
A. 2B. 1C. 8或1D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
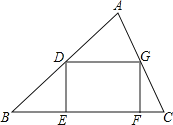
【题目】如图,在△ABC中,AB=400,BC=600,∠ABC=45°,在△ABC内作一个内接矩形DEGF(点E、F在边BC上,点D、G分别在边AB和AC上),则矩形DEFG的对角线EG最短为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市2016年中考,综合素质测试满分为100分.某校为了调查学生对于综合素质的掌握程度,在九年级学生中随机抽取了部分学生进行模拟测试,并将测试成绩绘制成下面两幅统计图.
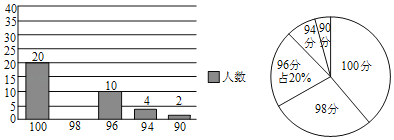
试根据统计图中提供的数据,回答下面问题:
(1)计算样本中,成绩为98分的学生有 ,并补全条形统计图.
(2)样本中,测试成绩的中位数是 分,众数是 分.
(3)若该校九年级共有2000名学生,根据此次模拟成绩估计该校九年级中考综合素质测试将有多少名学生可以获得满分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将抛物线y=-3x2先向左平移3个单位长度,再向下平移4个单位长度后所得到的抛物线的表达式为( )
A.y=-3(x+3)![]() 4B.y=-3(x3)
4B.y=-3(x3)![]() 4
4
C.y=-3(x+3)![]() +4D.y=-3(x3)
+4D.y=-3(x3) ![]() +4
+4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com