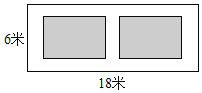
【题目】如图，某小区有一长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们面积之和为60平方米，两块绿地之间及周边留有宽度相等的人行通道，则人行道的宽度为（ ）米．
A. 2B. 1C. 8或1D. 8
科目：初中数学 来源： 题型：
【题目】定义：若抛物线
与抛物线
的开口大小相同，方向相反，且抛物线
经过
的顶点，我们称抛物线为的“友好抛物线”．
（1）若的表达式为
，求的“友好抛物线”的表达式；
（2）已知抛物线
为
的“友好抛物线”．求证：抛物线也是的“友好抛物线”；
（3）平面上有点
，
，抛物线为
的“友好抛物线”，且抛物线的顶点在第一象限，纵坐标为2，当抛物线与线段
没有公共点时，求
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列表格是某学校女子排球队队员年龄统计表：
年龄（岁） | 13 | 14 | 15 | 16 |
人数（人） | 1 | 2 | 4 | 5 |
（1）该排球队队员年龄的众数是 岁；
（2）事件“从该排球队随机选择一名队员，其年龄为13岁”发生的概率为 ；
（3）教练決定从年龄为13岁和14岁的A、B、C三名队员中，随机选取两名队员进行“接发球”训练，求队员A、B同时被选中的概率．（树状图或列表法）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，若点P的横坐标和纵坐标相等，则称点P为等值点．例如点
（1，1），(－2，－2)，(
，)，…，都是等值点．已知二次函数
的
图象上有且只有一个等值点
，且当m≤x≤3时，函数 
的最小值为－9，最大值为－1，则m的取值范围是__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝x2－4x＋3.
(1)用配方法求其图象的顶点C的坐标，并描述该函数的函数值随自变量的增减而变化的情况；
(2)求函数图象与x轴的交点A，B的坐标，及△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料:若
，求m、n的值.
解: 
，
，
，
.
根据你的观察，探究下面的问题:
（1）己知
，求
的值.
（2）已知△ABC的三边长a、b、c都是正整数，且满足
，求边c的最大值.
（3） 若己知
，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF．
（1）求证：△AED≌△CFD；
（2）求证：四边形AECF是菱形．
（3）若AD=3，AE=5，则菱形AECF的面积是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
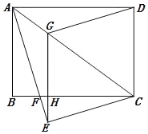
【题目】如图，把矩形ABCD沿AC折叠，使点D与点E重合，AE交BC于点F，过点E作EG∥CD交AC于点G，交CF于点H，连接DG．
（1）求证：四边形ECDG是菱形；
（2）若DG＝6，AG＝
，求EH的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，
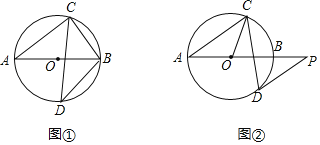
（1）如图①，若D为弧AB的中点，求∠ABC和∠ABD的大小；
（2）如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
