
分析 (1)根据已知方程的特点与解的关系即可写出方程的解;
(2)原方程可以变形为:x-1+$\frac{2}{x-1}$=c-1+$\frac{2}{c-1}$,把x-1当作一个整体,即可求解.
解答 解:(1)解是:x1=c,x2=$\frac{m}{c}$,
经检验:c和$\frac{m}{c}$是原方程的解;
(2)由x+$\frac{2}{x-1}$=c+$\frac{2}{c-1}$得x-1+$\frac{2}{x-1}$=c-1+$\frac{2}{c-1}$,
∴x-1=c-1,x-1=$\frac{2}{c-1}$,
∴x1=c,x2=$\frac{c+1}{c-2}$.
点评 本题主要考查了分式方程的解,解此题的关键是理解题意,认真审题,寻找规律.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k1<k2 | B. | k1=k2 | C. | k1>k2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
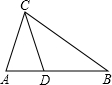 如图,下列四个条件:
如图,下列四个条件:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一次向右拐40°,第二次向右拐140° | |
| B. | 第一次向右拐40°,第二次向左拐40° | |
| C. | 第一次向左拐40°,第二次向右拐140° | |
| D. | 第一次向右拐140°,第二次向左拐40° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
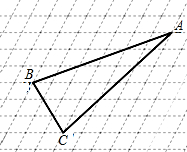 边长为a的菱形是由边长为a的正方形“形变”得到的,若这个菱形一组对边之间的距离为h,则称$\frac{a}{h}$为这个菱形的“形变度”.
边长为a的菱形是由边长为a的正方形“形变”得到的,若这个菱形一组对边之间的距离为h,则称$\frac{a}{h}$为这个菱形的“形变度”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com