
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:选择题
 如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )| A. | 105° | B. | 110° | C. | 100° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
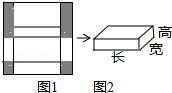 如图(1)是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图(2)所示的长方体纸盒.已知该长方体的宽是高的2倍,则它的体积是1000cm3.
如图(1)是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图(2)所示的长方体纸盒.已知该长方体的宽是高的2倍,则它的体积是1000cm3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3-a=a(a2-1) | B. | m2-2mn+n2=(m-n)2 | C. | x2y-xy2=xy(x-y) | D. | x2-y2=(x-y)(x+y) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com