
【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

【答案】(1) 111 ;(2) ∠A-∠C=2∠P,理由见解析;(3) ∠A+∠C=2∠P,理由见解析.
【解析】
(1)延长AD交BC于E,利用三角形外角的性质即可求解;
(2)∠A-∠C=2∠P,由三角形外角等于不相邻的两个内角的和以及(1)结论即可求解;
(3)∠A+∠C=2∠P,由(2)结论以及角平分线的性质即可得到.
(1)如图1,延长AD交BC于E,
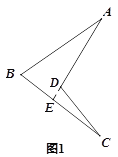
在△ABE中,∠AEC=∠A+∠B=28+72=100,
在△DEC中,∠ADC=∠AEC+∠C=100+11=111 ;
(2)∠A-∠C=2∠P,理由如下:
如图2,
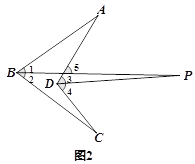
∠5=∠A+∠1,∠5=∠P+∠3
∴∠A+∠1=∠P+∠3
∵PB平分∠ABC,PD平分∠ADC
∴ ∠1=∠2,∠3=∠4
∴∠A+∠2=∠P+∠4
由(1)知∠4=∠2+∠P+∠C
∴∠A+∠2=∠P+∠2+∠P+∠C
∴∠A-∠C=2∠P
(3)∠A+∠C=2∠P,理由如下:
如图3,
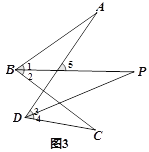
同(2)理知∠A+∠1=∠P+∠3,∠C+∠4=∠P+∠2
∴∠A+∠C+∠1+∠4=2∠P+∠2+∠3
∵PB平分∠ABC,PD平分∠ADC
∴ ∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
∴∠A+∠C=2∠P


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若AF=50,EC=7,则DE的长为( )
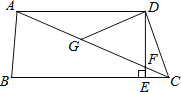
A. 14 B. 21 C. 24 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有( )
,则下列结论正确的有( )

①∠DCB=∠B;②CD=![]() AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点. 
(1)求∠D的度数;
(2)求证:AC2=ADCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC= ![]() .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F. 
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△A′B′C′在平面直角坐标系中的位置分别如图所示.
(1)分别写出下列各点的坐标:A_______;B_______;C_______;
(2)△ABC由△A′B′C′经过怎样的平移得到?
答:_____________________________________
(3)求△ABC面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com