
����Ŀ��ij�н���չ�ݽ��������ijУ�Բμ�ѡ�ε�ѧ���ijɼ���A��B��C��D�ĸ��ȼ�����ͳ�ƣ����������²�������ͳ�Ʊ�������ͳ��ͼ��
�ɼ��ȼ� | Ƶ�� | Ƶ�� |
A | 4 | n |
B | m | 0.51 |
C | ||
D | 15 |
��1����m��n��ֵ��
��2������C�ȼ�������Ӧ������Բ�ĽǵĶ�����
��3����֪�ɼ��ȼ�ΪA��4��ѧ������1��������3��Ů�����ִ��������ѡ2��ѧ������ѧУ�μ�ȫ�б��������ǡ��ѡ��һ������һŮ���ĸ���
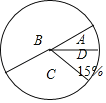
���𰸡���1��m��51��������n��0.04����2��108������3��![]()
��������
��1������������������ٸ���Ƶ��=Ƶ�����������ɵô𰸣�
��2�������C�ȼ�����������360������C�ȼ�������ռ�������ɵã�
��3���б��ó����еȿ��ܵ���������ҳ��պó鵽һ��һŮ��������������������ĸ��ʣ�
�⣺��1������������Ϊ15��15%��100��������
��m��100��0.51��51��������n��4��100��0.04��
��2��C�ȼ�����Ϊ100��4��51��15��30��������
����C�ȼ�������Ӧ������Բ�ĽǵĶ���Ϊ360���![]() ��108����
��108����
��3���б����£�
�� | Ů1 | Ů2 | Ů3 | |
�� | ������ | ��Ů���У� | ��Ů���У� | ��Ů���У� |
Ů1 | ���У�Ů�� | ������ | ��Ů��Ů�� | ��Ů��Ů�� |
Ů2 | ���У�Ů�� | ��Ů��Ů�� | ������ | ��Ů��Ů�� |
Ů3 | ���У�Ů�� | ��Ů��Ů�� | ��Ů��Ů�� | ������ |
�߹���12�ֵȿ��ܵĽ����ѡ��1��������1��Ů���������6�֣�
��P��ѡ��1��������1��Ů������![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
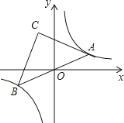
����Ŀ����ͼ����A��˫����![]() �ڵ�һ�����ϵ�һ���㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪб��������Rt��ABC����C�ڵڶ����ޣ����ŵ�A���˶�����C��λ��Ҳ���ϵı仯����ʼ����һ����ͼ�����˶�������������Ľ���ʽΪ ��
�ڵ�һ�����ϵ�һ���㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪб��������Rt��ABC����C�ڵڶ����ޣ����ŵ�A���˶�����C��λ��Ҳ���ϵı仯����ʼ����һ����ͼ�����˶�������������Ľ���ʽΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ20Ԫ����Ӫ���η��֣������۵�����25Ԫʱ��ÿ���������Ϊ250�������۵���ÿ����1Ԫ��ÿ����������ͼ���10��
��1��д���̳����������ľߣ�ÿ�����õ���������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ�����ľ�ÿ��������������
��3���̳���Ӫ���������������������A��B����Ӫ������
����A�����ľߵ����۵��۸��ڽ����Ҳ�����30Ԫ��
����B��ÿ��������������10������ÿ���ľߵ���������Ϊ25Ԫ
��Ƚ����ַ��������������ߣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��a��0������A����1��0����B��3��0����C��0����3�����㣬ֱ��l�������ߵĶԳ��ᣮ
��a��0������A����1��0����B��3��0����C��0����3�����㣬ֱ��l�������ߵĶԳ��ᣮ

��1���������ߵĺ�����ϵʽ��
��2�����P��ֱ��l�ϵ�һ�����㣬����P����A����B�ľ���֮�����ʱ�����P�����ꣻ
��3����MҲ��ֱ��l�ϵĶ��㣬����MACΪ���������Σ���ֱ��д�����з��������ĵ�M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
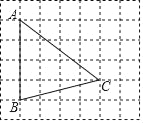
����Ŀ����ͼ����ÿ��С�����εı߳�Ϊ1�������У���A��B��C���ڸ���ϣ�
����AC�ij�����_____��
���������߶�AC����һ��D������AB2=ADAC��������ͼ��ʾ�������У����̶ȵ�ֱ�ߣ�������D������Ҫ˵����D��λ��������ҵ��ģ���Ҫ��֤����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ֱ��������ֽƬABC����ACB��90����AB��10��AC��6����DΪBC���ϵ���һ�㣬�ع���D��ֱ���۵���ʹֱ�Ƕ���C����б��AB�ϵĵ�E��������BDE��ֱ��������ʱ����CD�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
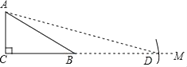
����Ŀ�������tan75���ֵ�������з�����ͼ�ɽ�����⣬��ͼ����Rt��ABC�У�AC��k����ACB��90�㣬��ABC��30�㣬�ӳ�CB����M��������BM�Ͻ�ȡ�߶�BD��ʹBD��AB������AD�����ݴ�ͼ�����tan75���ֵΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��Ҫ���ý�ʦ�칫����A��B����200�ף���֪2��A�����κ�1��B�����ι���2000Ԫ��1��A�����κ�3��B�����ι���3000Ԫ��
��1����A��B�������εĵ��ۣ�
��2������ҪA�����β�����120�ף�B�����β�����70�ף�ƽ��ÿ��������Ҫ�˷�10Ԫ���蹺��A������x��ʱ���ܷ���ΪyԪ����y��x�ĺ�����ϵʽ����ֱ��д��x��ȡֵ��Χ��
��3������ܷ������ٵĹ��÷�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com