
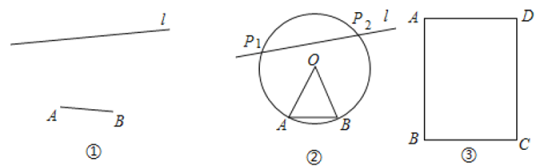
【题目】如图①,已知线段![]() 和直线
和直线![]() ,用直尺和圆规在
,用直尺和圆规在![]() 上作出所有的点
上作出所有的点![]() ,使得
,使得![]() ,如图②,小明的作图方法如下:
,如图②,小明的作图方法如下:
第一步:分别以点![]() ,
,![]() 为圆心,
为圆心,![]() 长为半径作弧,两弧在
长为半径作弧,两弧在![]() 上方交于点
上方交于点![]() ;
;
第二步:连接![]() ,
,![]() ;
;
第三步:以![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() ,交
,交![]() 于
于![]() ,
,![]() ;
;
所以图中![]() ,
,![]() 即为所求的点.
即为所求的点.
(1)在图②中,连接![]() ,
,![]() ,说明
,说明![]() ;
;
(方法迁移)
(2)如图③,用直尺和圆规在矩形![]() 内作出所有的点
内作出所有的点![]() ,使得
,使得![]() (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(深入探究)
(3)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上的点,若满足
边上的点,若满足![]() 的点
的点![]() 恰有两个,求
恰有两个,求![]() 的取值范围.
的取值范围.
(4)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 内一点,且
内一点,且![]() ,若点
,若点![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到点
到点![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)见解析;(3)2≤m<![]() +1;(4)
+1;(4)![]() .
.
【解析】
(1)先根据等边三角形得:∠AOB=60°,则根据圆周角定理可得:∠AP1B=30°;
(2)先作等腰直角三角形BEC、BFC,再作△EBC的外接圆,可得圆心角∠BOC=90°,则弧BC所对的圆周角都是45°;
(3)先确定⊙O,根据同弧所对的圆周角相等可得AD在四边形GEFH内部时符合条件;
(4)先确定⊙O,根据圆周角定理正确画出∠BPC=135°,利用勾股定理求OF的长,知道A、P、O在同一直线上时,AP最小,则PQ的值最小,求AE的长,即是AP的长,可得PQ的最小值.
解:(1)∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
由题意得:∠AP1B=![]() ∠AOB=30°;
∠AOB=30°;
(2)如图,①以B、C为圆心,以BC为半径作圆,交AB、DC于E、F,
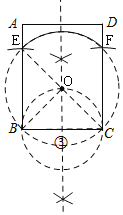
②作BC的中垂线,连接EC,交于O,
③以O为圆心,OE为半径作圆,
则弧EF上所有的点(不包括E、F两点)即为所求;
(3)如图④,同理作⊙O,
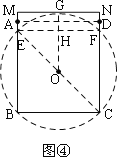
∵BE=BC=2,
∴CE=2![]() ,
,
∴⊙O的半径为![]() ,即OE=OG=
,即OE=OG=![]() ,
,
∵OG⊥EF,
∴EH=1,
∴OH=1,
∴GH=![]() -1,
-1,
∴BE≤AB<MB,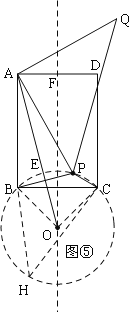
∴2≤m<2+![]() -1,即2≤m<
-1,即2≤m<![]() +1,
+1,
故答案为:2≤m<![]() +1;
+1;
(4)如图⑤,构建⊙O,使∠COB=90°,在弧BC上取一点H,则∠CHB=45°
∴∠CPB=135°,
由旋转得:△APQ是等腰直角三角形,
∴PQ=![]() AP,
AP,
∴PQ取最小值时,就是AP取最小值,
当P与E重合时,即A、P、O在同一直线上时,AP最小,则PQ的值最小,
在Rt△AFO中,AF=1,OF=3+1=4,
∴AO=![]() ,
,
∴AE=![]() =AP,
=AP,
∴PQ=![]() AP=
AP=![]() (
(![]() )=
)=![]() .
.
故答案为:![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
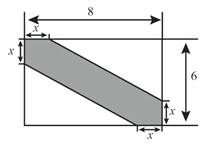
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
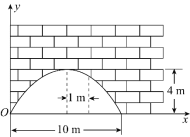
【题目】有一个抛物线形的拱形桥洞,桥面离水面的距离为5.6米,桥洞离水面的最大高度为![]() ,跨度为
,跨度为![]() ,如图所示,把它的图形放在直角坐标系中.
,如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式.
(2)如图,在对称轴右边![]() 处,桥洞离桥面的高是多少?
处,桥洞离桥面的高是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
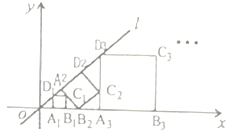
【题目】如图,在平面直角坐标系中,直线![]() 为正比例函数
为正比例函数![]() 的图象,点
的图象,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 轴于点
轴于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,…,按此规律操作下所得到的正方形
,…,按此规律操作下所得到的正方形![]() 的面积是
的面积是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
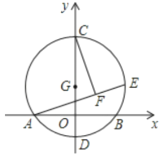
【题目】如图,以![]() 为圆心,半径为2的圆与
为圆心,半径为2的圆与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 为圆
为圆![]() 上一动点,
上一动点,![]() 于
于![]() ,当点
,当点![]() 在圆
在圆![]() 的运动过程中,线段
的运动过程中,线段![]() 的长度的最小值为__________.
的长度的最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
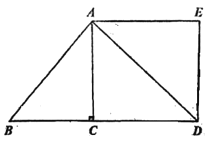
【题目】如图,在Rt![]() 中,∠ACB=90°,
中,∠ACB=90°,![]() ,AC=4;D是BC的延长线上一个动点,∠EDA=∠B,AE//BC.
,AC=4;D是BC的延长线上一个动点,∠EDA=∠B,AE//BC.
(1)找出图中的相似三角形,并加以证明;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当![]() 为等腰三角形时,求AE的长.
为等腰三角形时,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com