
【题目】若3<x<4,则(x-3)(4-x)_____0(填“>”“<”或“=”).
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
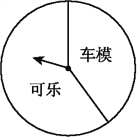
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C移动,同时,点Q在线段CA上由点C向点A移动.若点Q的移动速度与点P的移动速度相同,则经过秒后,△BPD≌△CQP. 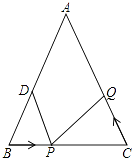
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC的外侧作直线BD,作点A关于直线BD的对称点A′,连接AA′交直线BD于点E,连接A′C交直线BD于点F.
(1)依题意补全图1,已知∠ABD=30°,求∠BFC的度数; 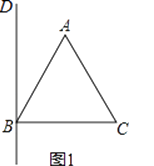
(2)如图2,若60°<∠ABD<90°,判断直线BD和A′C相交所成的锐角的度数是否为定值?若是,求出这个锐角的度数;若不是,请说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )
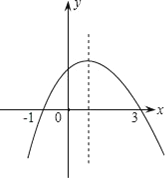
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
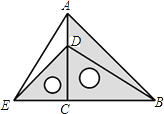
【答案】BF⊥AE,理由详见解析.
【解析】BD=AE ,BD⊥AE.延长BD交AE于F ,证△BCD≌△ACE,可得BD=AE ,BD⊥AE .
∵CE=CD,CA=CB,∠ACE=∠BCD=90°,∴△BCD≌△ACE,∴BD=AE,∠CBD=∠CAE,∵∠CAE+∠AEC=90°,∴∠CBD+∠AEC=90°,∴∠BFE=90°,即BD⊥AE.
【题型】解答题
【结束】
24
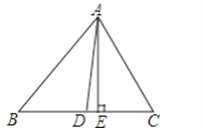
【题目】在△ABC中,已知∠B=50°,∠C=60°,AE⊥BC于E,AD平分∠BAC;求:∠DAE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com