
分析 (1)先把抛物线解析式化成顶点式,确定出顶点坐标,即可得出结论;
(2)令抛物线中的y=0用一元二次方程根的判别式即可得出结论;
(3)先确定出n的值,进而得出点Q的坐标,即可确定出点A,B坐标,最后确定出AQ,BQ,即可.
解答 解:(1)∵抛物线y=ax2-2anx+an2+n+3=a(x-n)2+(n+3),
∴抛物线P(n,n+3),
∵顶点P在一条定直线l上,
令n=x,n+3=y,
∴y=x+3,
即:直线l的解析式为y=x+3,
(2)抛物线与x轴有唯一的公共点,
令y=0,即:ax2-2anx+an2+n+3=0,
∴△=(-2an)2-4a×(an2+n+3)=-4a(n+3)=0,
∵任意非零实数a,
∴n+3=0,
∴n=-3,
∴抛物线与x轴有唯一的公共点,此时n的值为-3,
(3)由(1)知,P(n,n+3),
∵点P在x轴上,
∴n+3=0,
∴n=-3,
∴抛物线y=a(x+3)2,①
∵直线l的解析式为y=x+3②,
联立①②得Q(-3+$\frac{1}{a}$,$\frac{1}{a}$),
∵过点Q作y轴的平行线,交x轴于点B,
∴BQ=|$\frac{1}{a}$|,
∵过点Q作x轴的平行线,交抛物线于点A,
∴a(x+3)2=$\frac{1}{a}$,
∴x=-3±$\frac{1}{a}$,
∴A(-3-$\frac{1}{a}$,$\frac{1}{a}$),
∵Q(-3+$\frac{1}{a}$,$\frac{1}{a}$),
∴AQ=|-3+$\frac{1}{a}$-(-3-$\frac{1}{a}$)|=|$\frac{2}{a}$|
∴$\frac{AQ}{BQ}=\frac{|\frac{2}{a}|}{|\frac{1}{a}|}$=2.
点评 此题是二次函数综合题,主要考查了配方法,抛物线的顶点坐标的确定,二次函数和一元二次方程的关系,根的判别式,函数图象的交点坐标,解本题的关键是确定出n的值.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:填空题
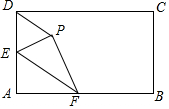 如图,在矩形ABCD中,AB=6,AD=3,点E、F分别在AD、AB线段上,将△AEF沿EF翻折,使得点A落在矩形ABCD内部P点,连接PD,则PD的最小值是3$\sqrt{5}$-6.
如图,在矩形ABCD中,AB=6,AD=3,点E、F分别在AD、AB线段上,将△AEF沿EF翻折,使得点A落在矩形ABCD内部P点,连接PD,则PD的最小值是3$\sqrt{5}$-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小强从A到B共有三条路线:①A→B;②A→D→B;③A→C→B.在不考虑其他因素的情况下,我们可以肯定小明会走路线①.理由是两点之间,线段最短.
小强从A到B共有三条路线:①A→B;②A→D→B;③A→C→B.在不考虑其他因素的情况下,我们可以肯定小明会走路线①.理由是两点之间,线段最短.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com