
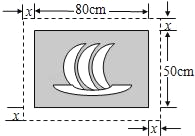
【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
(1)求出y关于x的函数解析式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽应为多少cm时,这幅挂图的面积最大?求出最大面积的值.
【答案】(1)y=4x2+260x+4000(1≤x≤2);(2)金色纸边的宽为2cm时,这幅挂图的面积最大,最大面积的值为4536cm2.
【解析】
(1)用含x的代数式表示出镶纸边后矩形的长和宽,根据矩形的面积公式即可得出y关于x的函数解析式,结合题意标明x的取值范围即可;
(2)根据二次函数的性质确定在自变量的取值范围内函数的单调性,由此即可解决最值问题.
(1)镶金色纸边后风景画的长为(80+2x)cm,宽为(50+2x)cm,
∴y=(80+2x)(50+2x)=4x2+260x+4000(1≤x≤2).
(2)∵二次函数y=4x2+260x+4000的对称轴为x=﹣![]() ,
,
∴在1≤x≤2上,y随x的增大而增大,
∴当x=2时,y取最大值,最大值为4536.
答:金色纸边的宽为2cm时,这幅挂图的面积最大,最大面积的值为4536cm2.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
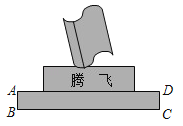
【题目】如图是某中学校园内新建的一座腾飞雕塑,数学老师给八年级的两个数学社团布置了验证雕塑底座正面的边AB和边CD是否分别垂直于底边BC的作业.老师给巧手社团配备的工具只有卷尺,给敏思社团只配备了一把20cm长的刻度尺他们能完成任务吗?如果能,请给出测量方案;如果不能需要增加哪些测量工具?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品零售店为食品厂代销一种面包,未售出的面包可以退回厂家.经统计销售情况发现,当这种面包的销售单价为7角时,每天卖出160个.在此基础上.单价每提高1角时,该零售店每天就会少卖出20个面包.设这种面包的销售单价为x角(每个面包的成本是5角).零售店每天销售这种面包的利润为y角.
(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
(2)求x与y之间的函数关系式:
(3)当这种面包的销售单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
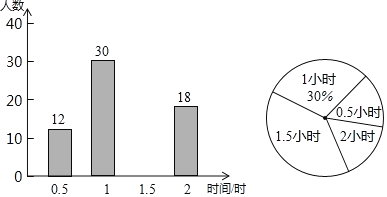
【题目】2019年8月,第18届世界警察和消防员运动会在成都举行.我们在体育馆随机调查了部分市民当天的观赛时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
(1)将条形统计图补充完整;
(2)求抽查的市民观赛时间的众数、中位数;
(3)求所有被调查市民的平均观赛时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
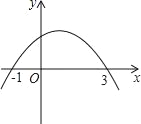
【题目】如图,已知二次函数的图象与x轴的两个交点分别为(﹣1,0),(3,0),对于下列结论:①2a+b=0;②abc<0;③a+b+c>0;④当x>1时,y随x的增大而减小;其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com