
【题目】如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F. 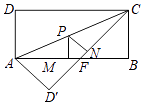
(1)求线段AF的长.
(2)求△AFC的面积.
(3)点P为线段AC(不含点A、C)上任意一点,PM⊥AB于点M,PN⊥CD′于点N,试求PM+PN的值.
【答案】
(1)解:∵四边形ABCD是矩形,
∴∠B=90°,AB∥CD,
∴∠DCA=∠BAC,
∵矩形沿AC折叠,点D落在点E处,
∴△ACD≌△ACE,
∴∠DCA=∠ECA,
∴∠BAC=∠ECA,
∴AF=CF,
设AF=CF=x,则BF=8﹣x,
在Rt△BCF中,根据勾股定理得:BC2+BF2=CF2,
即42+(8﹣x)2=x2,
解得:x=5,
∴AF=5;
(2)解:S△ACF= ![]() AFBC=
AFBC= ![]() ×5×4=10;
×5×4=10;
(3)解:连接PF,
![]() ×AF×PM+
×AF×PM+ ![]() ×CF×PN=S△ACF=10,
×CF×PN=S△ACF=10,
∴PM+PN=4.

【解析】(1)根据矩形的性质和翻折变换的性质得到AF=CF,设AF=x,根据勾股定理列出方程,解方程即可求出AF;(2)根据三角形面积公式计算即可;(3)连接PF,根据三角形的面积公式解答即可.
【考点精析】根据题目的已知条件,利用矩形的性质和翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明和小红两人周末去爬山,小红先出发,中间休息了一段时间,然后按休息前的进度继续前进,最后比小明迟到达山顶.设他们俩从山脚出发后所用的时间t(分钟)与所走的路程S(米)之间的函数关系如图所示: 
(1)根据图象小明登山的速度为米/分,小红的登山速度为米/分.
(2)求出BC段图象的函数关系式,并写出自变量的取值范围.
(3)小明到达山顶后,小红还有多少米到山顶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=x3﹣2y3+3x2y+xy2﹣3xy+4,B=y3﹣x3﹣4x2y﹣3xy﹣3xy2+3,C=y3+x2y+2xy2+6xy﹣6,试说明对于x、y、z的任何值A+B+C是常数.
查看答案和解析>>
科目:初中数学 来源: 题型:
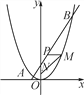
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反,若汽车第一次是右拐40°,则第二次应该是( )
A.左拐40°B.左拐50°C.左拐140°D.右拐 140°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com