
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

【答案】(1)y=﹣0.1x+8(30≤x≤60)(2)w= (3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
(3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
【解析】试题分析:(1)由图象知,当30≤x≤60时,图象过(60,2)和(30,5),运用待定系数法求解析式即可;
(2)根据销售产品的纯利润=销售量×单个利润,分30≤x≤60和60<x≤80列函数表达式;
(3)当30≤x≤60时,运用二次函数性质解决,当60<x≤80时,运用反比例函数性质解答.
试题解析:(1)当x=60时,y=![]() =2,
=2,
∴当30≤x≤60时,图象过(60,2)和(30,5),
设y=kx+b,则![]() ,
,
解得: ![]() ,
,
∴y=﹣0.1x+8(30≤x≤60);
(2)根据题意,当30≤x≤60时,W=(x﹣20)y﹣50=(x﹣20)(﹣0.1x+8)﹣50=![]() +10x﹣210,
+10x﹣210,
当60<x≤80时,W=(x﹣20)y﹣50=(x﹣20)![]() ﹣50=
﹣50=![]() +70,
+70,
综上所述:W= ;
;
(3)当30≤x≤60时,W=![]() +10x﹣210=
+10x﹣210=![]() ,
,
当x=50时, ![]() =40(万元);
=40(万元);
当60<x≤80时,W=![]() +70,
+70,
∵﹣2400<0,W随x的增大而增大,
∴当x=80时, ![]() =
=![]() +70=40(万元),
+70=40(万元),
答:当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元.


科目:初中数学 来源: 题型:
【题目】下列从左到右的变形中是因式分解的有( )
①x2﹣y2﹣1=(x+y)(x﹣y)﹣1;
②x3+x=x(x2+1);
③(x﹣y)2=x2﹣2xy+y2;
④x2﹣9y2=(x+3y)(x﹣3y).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试,计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格、达到9分或10分以上为优秀.这20位同学的成绩与统计数据如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表中,a= ,b= ;
(2)有人说二班的及格率、优秀率高于一班,所以二班的成绩比一班好,但也有人坚持认为一班成绩比二班好,请你给出支持一班成绩好的两条理由;
(3)若从这两班获满分的同学中随意抽1名同学参加“汉字听写大赛”,求参赛同学恰好是一班同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“爱我海珠,创卫同行”的活动,倡议学生利用双休日在海珠湿地公园参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整.
(2)抽查的学生劳动时间的众数为 , 中位数为 .
(3)已知全校学生人数为1200人,请你估算该校学生参加义务劳动1小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F. 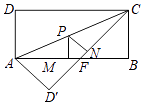
(1)求线段AF的长.
(2)求△AFC的面积.
(3)点P为线段AC(不含点A、C)上任意一点,PM⊥AB于点M,PN⊥CD′于点N,试求PM+PN的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com