
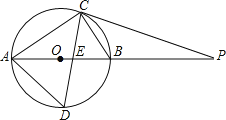
【题目】如图⊙O的直径AB=10cm,弦BC=6cm,∠ACB的平分线交⊙O于D,交AB于E,P是AB延长线上一点,且PC=PE.
(l)求证:PC是⊙O的切线;
(2)求AC、AD的长.
【答案】(1)见解析;(2)AC=8cm,AD=5![]() cm
cm
【解析】
(1)连结OC,由PC=PE得∠PCE=∠PEC,利用三角形外角性质得∠PEC=∠EAC+∠ACE=∠EAC+45°,加上∠CAB=90°﹣∠ABC,∠ABC=∠OCB,于是可得到∠PCE=90°﹣∠OCB+45°=90°﹣(∠OCE+45°)+45°,则∠OCE+∠PCE=90°,于是根据切线的判定定理可得PC为⊙O的切线;
(2)连结BD,如图,根据圆周角定理由AB为直径得∠ACB=90°,则可利用勾股定理计算出AC=8;由DC平分∠ACB得∠ACD=∠BCD=45°,根据圆周角定理得∠DAB=∠DBA=45°,则△ADB为等腰直角三角形,由勾股定理即可得出AD的长.
(1)证明:连结OC,如图所示:
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠EAC+∠ACE=∠EAC+45°,
而∠CAB=90°﹣∠ABC,∠ABC=∠OCB,
∴∠PCE=90°﹣∠OCB+45°=90°﹣(∠OCE+45°)+45°,
∴∠OCE+∠PCE=90°,
即∠PCO=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(2)连结BD,如图所示,
∵AB为直径,
∴∠ACB=90°,
在Rt△ACB中,AB=10cm,BC=6cm,
∴AC=![]() =8(cm);
=8(cm);
∵DC平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠DAB=∠DBA=45°
∴△ADB为等腰直角三角形,
∴![]() (cm).
(cm).


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】重庆市某商场通过互联网销售某品牌新型台灯,第一周的总销售额为4000元,第二周的总销售额为4520元,第二周比第一周多售出13盏台灯.
(1)求每盏台灯的售价;
(2)该公司在第三周将每盏台灯的售价降低了![]() ,并预计第三周能售出140盏灯,恰逢期末考试,极大的提高了中学生使用台灯的数量,该款台灯在第三周的销量比预计的140盏还多了
,并预计第三周能售出140盏灯,恰逢期末考试,极大的提高了中学生使用台灯的数量,该款台灯在第三周的销量比预计的140盏还多了![]() .已知每盏台灯的成本为16元,该公司第三周销售台灯的总利润为5040元,求
.已知每盏台灯的成本为16元,该公司第三周销售台灯的总利润为5040元,求![]() 的值(其中
的值(其中![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2).
x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2).
(1)求抛物线的表达式,并用配方法求出顶点D的坐标;
(2)若点E是点C关于抛物线对称轴的对称点,求tan∠CEB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2kx+![]() k2-2=0.
k2-2=0.
(1)求证:不论k为何值,方程总有两不相等实数根.
(2)设x1,x2是方程的根,且 x12-2kx1+2x1x2=5,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
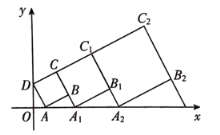
【题目】在平面直角坐标系中,正方形ABCD 的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1CC1B1,延长C1B1交x轴于点A2,作正方形A2C1C2B2,…,按照这样的规律作正方形,则点B2019的纵坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
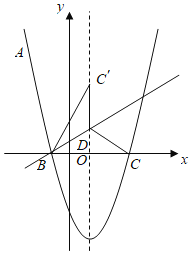
【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,
两点,
(1)抛物线的函数表达式;
(2)点![]() 在抛物线的对称轴上,且位于
在抛物线的对称轴上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿沿直线
沿沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在抛物线的对称轴上,求点
恰好落在抛物线的对称轴上,求点![]() 和点
和点![]() 的坐标;
的坐标;
(3)设![]() 是抛物线上位于对称轴右侧的一点,点
是抛物线上位于对称轴右侧的一点,点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
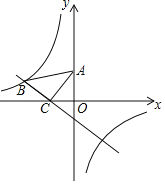
【题目】如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,点C坐标为(﹣1,0),点A坐标为(0,2).一次函数y=kx+b的图象经过点B、C,反比例函数y=![]() 的图象经过点B.
的图象经过点B.
(1)求一次函数和反比例函数的关系式;
(2)直接写出当x<0时,kx+b﹣![]() <0的解集;
<0的解集;
(3)在x轴上找一点M,使得AM+BM的值最小,直接写出点M的坐标和AM+BM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
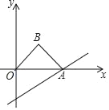
【题目】如图,直线y=![]() x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=
x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=![]() x﹣2上时,则△OAB平移的距离是_____.
x﹣2上时,则△OAB平移的距离是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com