
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 上的两点,过
上的两点,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,![]() 为
为![]() 上的任意一点,若
上的任意一点,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值是__________.
的最小值是__________.

【答案】![]() .
.
【解析】
先由MN=10求出⊙O的半径,再连接OA、OB,由勾股定理得出OD、OC的长,作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=3,过点B′作AC的垂线,交AC的延长线于点E,证出△AB′E是等腰直角三角形即可得出结果.
解:∵MN=10,
∴⊙O的半径=5,
连接OA、OB,
在Rt△OBD中,OB=5,BD=3,
∴OD=![]() ,
,
同理,在Rt△AOC中,OA=5,AC=4,
∴OC=![]() ,
,
∴CD=4+3=7,
作点B关于MN的对称点B′,连接AB′,
则AB′即为PA+PB的最小值,B′D=BD=3,
过点B′作AC的垂线,交AC的延长线于点E,如图所示:
则四边形CDB′E是矩形,
∴B′E=CD=7,CE=DB′=DB=3,
∵AE=AC+CE=4+3=7,B′E=CD=7,
∴△AB′E是等腰直角三角形,
∴AB′=![]() AE=
AE=![]() ,
,
故答案为:![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有四张质地均匀,大小完全相同的卡片,在其正面分别标有数字﹣1,﹣2,2,3,把卡片背面朝上洗匀,从中随机抽出一张后,不放回,再从中随机抽出一张,则两次抽出的卡片所标数字之和为正数的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络购物已成为新的消费方式,催生了快递行业的高速发展,某小型的快递公司,今年5月份与7月份完成快递件数分别为5万件和5.832份万件,假定每月投递的快递件数的增长率相同.
(1)求该快递公司投递的快递件数的月平均增长率;
(2)如果每个快递小哥平均每月最多可投递0.8万件,公司现有8个快递小哥,按此快递增长速度,不增加人手的情况下,能否完成今年9月份的投递任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
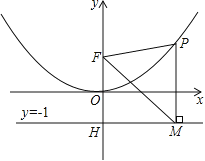
【题目】二次函数图象的顶点在原点O,经过点A(1,![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
(1)求抛物线的函数解析式;
(2)若D是抛物线位于第一象限上的动点,求△BCD面积的最大值及此时点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉市雾霾天气严重,环境治理已刻不容缓,武汉市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台,经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台,若供应商规定这种空气净化器售价不低于330元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量![]() (台)与售价
(台)与售价![]() (元/台)之间的函数关系式.
(元/台)之间的函数关系式.
(2)当售价![]() (元/台)定为多少时,商场每月销售这种空气净化器所获得的利润
(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
(3)当售价![]() (元/台)满足什么条件时,商场每月销售这种空气净化器所获得的利润
(元/台)满足什么条件时,商场每月销售这种空气净化器所获得的利润![]() (元)不低于70000元?
(元)不低于70000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
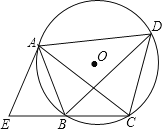
【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,BA平分∠EBD,AE=AB.
(1)求证:AC=AD.
(2)当![]() ,AD=6时,求CD的长.
,AD=6时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
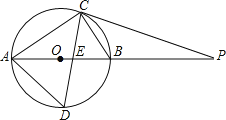
【题目】如图⊙O的直径AB=10cm,弦BC=6cm,∠ACB的平分线交⊙O于D,交AB于E,P是AB延长线上一点,且PC=PE.
(l)求证:PC是⊙O的切线;
(2)求AC、AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形的一条对角线将这个四边形分成两个三角形,如果这两个三角形相似(不全等),那么我们将这条对角线叫做这个四边形的相似对角线.
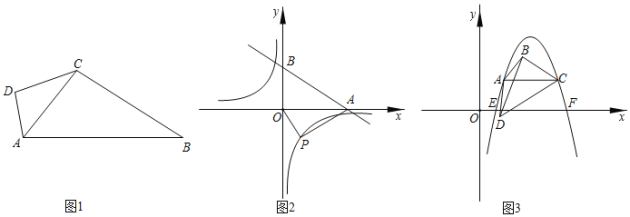
(1)如图1,四边形ABCD中,∠DAB=100°,∠DCB=130°,对角线AC平分∠DAB,求证:AC是四边形ABCD的相似对角线;
(2)如图2,直线![]() 分别与x,y轴相交于A,B两点,P为反比例函数y=
分别与x,y轴相交于A,B两点,P为反比例函数y=![]() (k<0)上的点,若AO是四边形ABOP的相似对角线,求反比例函数的解析式;
(k<0)上的点,若AO是四边形ABOP的相似对角线,求反比例函数的解析式;
(3)如图3,AC是四边形ABCD的相似对角线,点C的坐标为(3,1),AC∥x轴,∠BCA=∠DCA=30°,连接BD,△BCD的面积为![]() .过A,C两点的抛物线y=ax2+bx+c(a<0)与x轴交于E,F两点,记|m|=AC+1,若直线y=mx与抛物线恰好有3个交点,求实数a的值.
.过A,C两点的抛物线y=ax2+bx+c(a<0)与x轴交于E,F两点,记|m|=AC+1,若直线y=mx与抛物线恰好有3个交点,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com