
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
(1)求抛物线的函数解析式;
(2)若D是抛物线位于第一象限上的动点,求△BCD面积的最大值及此时点D的坐标.

【答案】(1) 抛物线的函数解析式为y=﹣![]() x2+
x2+![]() x+2;(2)4;D(2,3).
x+2;(2)4;D(2,3).
【解析】
(1)把A与C坐标代入抛物线解析式求出b与c的值,确定出解析式即可;
(2)连接OD,设出D坐标,四边形OCDB的面积等于三角形OCD面积+三角形OBD面积,表示出三角形BCD面积S与m的二次函数解析式,求出最大面积及D坐标即可.
(1)将点A(﹣1,0),点C(0,2)纵、横坐标分别代入y=﹣![]() x2+bx+c得:
x2+bx+c得:
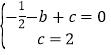 ,
,
解得:![]() ,
,
则抛物线的函数解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)连接OD,则有B(4,0),设D(m,﹣![]() m2+
m2+![]() m+2),
m+2),
∵S四边形OCDB﹣S△OCD﹣S△OBD=![]() ×2m+
×2m+![]() ×4(﹣
×4(﹣![]() m2+
m2+![]() m+2)=﹣m2+4m+4,
m+2)=﹣m2+4m+4,
∴S△BCD=S四边形OCDB﹣S△OBC=﹣m2+4m+4﹣![]() ×4×2=﹣m2+4m=﹣(m﹣2)2+4,
×4×2=﹣m2+4m=﹣(m﹣2)2+4,
当m=2时,S△BCD取得最大值4,
此时yD=﹣![]() ×4+
×4+![]() ×2+2=3,即D(2,3).
×2+2=3,即D(2,3).


科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年暑假,小丽爸爸的同事送给她爸爸一张北京故宫的门票,她和哥哥两人都很想去参观,可门票只有一张.读九年级的哥哥想了一个办法,他拿了八张扑克牌,将数字为1,2,3,5的四张牌给小丽,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小利哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌上的数字相加,如果和为偶数,和小丽去;如果和为奇数,则哥哥去.
(1)请用画树状图或列表的方法求小丽去北京故宫参观的概率;
(2)哥哥设计的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
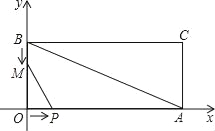
【题目】如图,在平面直角坐标系xOy中,已知矩形OACB的边OA,OB分别在x轴上和y轴上,线段OA=24,OB=12;点P从点O开始沿OA边匀速移动,点M从点B开始沿BO边匀速移动.如果点P,点M同时出发,它们移动的速度相同都是1个单位/秒,设经过x秒时(0≤x≤12),△POM的面积为y.
(1)求直线AB的解析式;
(2)求y与x的函数关系式;
(3)连接矩形的对角线AB,当x为何值时,以M、O、P为顶点的三角形等于△AOB面积的![]() ;
;
(4)当△POM的面积最大时,将△POM沿PM所在直线翻折后得到△PDM,试判断D点是否在直线AB上,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一条抛物线的对称轴是直线x=1;它与x轴相交于A,B两点(点A在点B的左边),且线段AB的长是4;它还与过点C(1,﹣2)的直线有一个交点是D(2,﹣3).
(1)求这条直线的函数解析式;
(2)求这条抛物线的函数解析式;
(3)若这条直线上有P点,使S△PAB=12,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x(x-2)=x-2①与一元一次方程2x+1=2a-x②.
(1)若方程①的一个根是方程②的根,求a的值;
(2)若方程②的根不小于方程①两根中的较小根且不大于方程①两根中的较大根,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从某点![]() 点处出发在一直线上来回爬行,假定向右爬行的路程记为正数,左爬行的路程为负数,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-11.
点处出发在一直线上来回爬行,假定向右爬行的路程记为正数,左爬行的路程为负数,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-11.
(1)小虫最后是否回到出发点![]() 点?如果不在,请说出小虫的位置;
点?如果不在,请说出小虫的位置;
(2)小虫离开出发点![]() 点最远时是 厘米;
点最远时是 厘米;
(3)在爬行过程中,如果每爬1厘米奖励两粒芝麻,则小虫共得多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
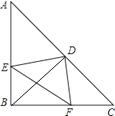
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边中点,过D点作DE⊥DF,交AB于E,交BC于F,连接BD.
(1)求证:△CDF≌△BED
(2)若AE=4,FC=3,求AB长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com