
����Ŀ���ı��ε�һ���Խ��߽�����ı��ηֳ����������Σ��������������������(��ȫ��)����ô���ǽ������Խ��߽�������ı��ε����ƶԽ��ߣ�
(1)��ͼ1���ı���ABCD�У���DAB��100������DCB��130�����Խ���ACƽ�֡�DAB����֤��AC���ı���ABCD�����ƶԽ��ߣ�
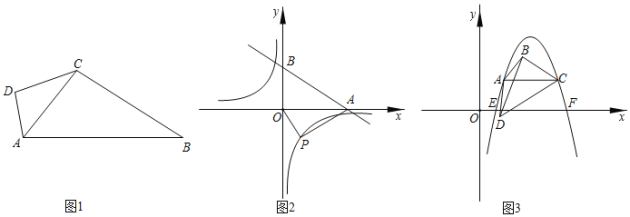
(2)��ͼ2��ֱ��![]() �ֱ���x��y���ཻ��A��B���㣬PΪ����������y��
�ֱ���x��y���ཻ��A��B���㣬PΪ����������y��![]() (k��0)�ϵĵ㣬��AO���ı���ABOP�����ƶԽ��ߣ����������Ľ���ʽ��
(k��0)�ϵĵ㣬��AO���ı���ABOP�����ƶԽ��ߣ����������Ľ���ʽ��
(3)��ͼ3��AC���ı���ABCD�����ƶԽ��ߣ���C������Ϊ(3��1)��AC��x�ᣬ��BCA����DCA��30��������BD����BCD�����Ϊ![]() ����A��C�����������y��ax2+bx+c(a��0)��x�ύ��E��F���㣬��|m|��AC+1����ֱ��y��mx��������ǡ����3�����㣬��ʵ��a��ֵ��
����A��C�����������y��ax2+bx+c(a��0)��x�ύ��E��F���㣬��|m|��AC+1����ֱ��y��mx��������ǡ����3�����㣬��ʵ��a��ֵ��
���𰸡���1������������2��y����![]() ��y����
��y����![]() ��y����
��y����![]() ��y����
��y����![]() ����3��a����
����3��a����![]() ��
��![]() ��
��
��������
��1����ͼ1�����ACD���������ACB��130�����������B��180������BAC����ACB��180����50������130��������������������⣻
��2���֡�APOΪֱ�ǡ���OAPΪֱ������������ֱ���⼴�ɣ�
��3��CH��![]() BC����BH��
BC����BH��![]() BC����BCD�������
BC����BCD�������![]() CDBH��
CDBH��![]() CD��
CD��![]() HB��
HB��![]() ����CDBC��4������BAC�ס�ACD����CD2��BCCD��4����CD��2�����A��1��1�����������ߵı���ʽΪ��y��ax2+��4a+3��x+3a+1��AC��1����m����3����ֱ�ߵı���ʽΪ��y����3x��ֱ��y����3x�����������������㣬��ֱ��y��mx��������ǡ����3�����㣬��ֱ��y��3x����������һ�����㣬������⣮
����CDBC��4������BAC�ס�ACD����CD2��BCCD��4����CD��2�����A��1��1�����������ߵı���ʽΪ��y��ax2+��4a+3��x+3a+1��AC��1����m����3����ֱ�ߵı���ʽΪ��y����3x��ֱ��y����3x�����������������㣬��ֱ��y��mx��������ǡ����3�����㣬��ֱ��y��3x����������һ�����㣬������⣮
�⣺��1����ͼ1�����ACD���������ACB��130��������
���B��180������BAC����ACB��180����50������130��������������
�ڡ�ABC�͡�ACD�У���B����ACD����BAC����CAD��
���ABC�ס�ACD��
��AC���ı���ABCD�����ƶԽ��ߣ�
��2���ٵ���APOΪֱ��ʱ��
����OAP��30��ʱ��
����P��PH��x���ڵ�H��
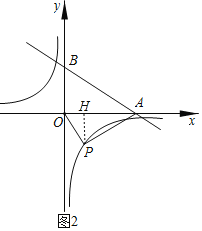
��OH��x����HP��![]() x��HA��3x����x+3x��4��
x��HA��3x����x+3x��4��
��ã�x��1���ʵ�P��1����![]() ������k����
������k����![]() ��
��
����AOP��30��ʱ��
ͬ���ɵã�k����3![]() ��
��
�ڵ���OAPΪֱ��ʱ��
����OPA��30��ʱ��
��P��4����4![]() ����k����16
����k����16![]() ��
��
����AOP��30��ʱ��OA��AO����OAP����AOB��90������AOP����OAB��30��
���OAP�ա�AOB�����������ƶԽ��ߵĶ��壬����ȥ��
���ϣ������������ı���ʽΪ��y����![]() ��y����
��y����![]() ��y����
��y����![]() ��
��
��3����ͼ3������B��BH��CD�ڵ�H�����CBH��60������BCD��30����

��CH��![]() BC����BH��
BC����BH��![]() BC��
BC��
��BCD�������![]() CDBH��
CDBH��![]() CD��
CD��![]() BC��
BC��![]() ����CDBC��4
����CDBC��4
����BAC�ס�ACD����CA2��BCCD��4����CA��2��
���A��1��1��������C��3��1����
����A��C��������������߱���ʽ����ã�
�����ߵı���ʽΪ��y��ax2��4ax+3a+1��
AC��2����m����3��
��ֱ�ߵı���ʽΪ��y����3x��
ֱ��y����3x�����������������㣬��ֱ��y��mx��������ǡ����3�����㣬
��ֱ��y��3x����������һ�����㣬
����ֱ��y��3x�������ߵı���ʽ�������ã�ax2����4a+3��x+3a+1��0��
������4a+3��2��4a��3a+1����0��
��ã�a����![]() ��
��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1����![]() �Ƶ�
�Ƶ�![]() ��ת
��ת![]() �õ�
�õ�![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2����ͼ2����![]() �DZ�
�DZ�![]() ������һ�㣨��
������һ�㣨��![]() ���
���![]() ��
��![]() ���غϣ�������
���غϣ�������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ������
������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
����֤��![]() ��
��
�ڵ���![]() ��
��![]() ���е�ʱ��ǡ��
���е�ʱ��ǡ��![]() ��
��![]() ������������
Ϊ������������![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
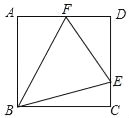
����Ŀ����ͼ����������ABCD�У�F��AD���е㣬E��CD��һ�㣬��FBE��45������tan��FEB��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
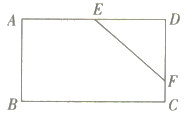
����Ŀ����ͼ���ھ���![]() �У�
�� ![]() ��
��![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() �ϣ���
�ϣ���![]() ���ڴ˾����ϴ���һ��
���ڴ˾����ϴ���һ��![]() ��ʹ��
��ʹ��![]() �ǵ��������Σ����
�ǵ��������Σ����![]() �ĸ����ǣ� ��
�ĸ����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
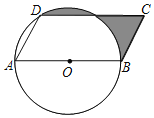
����Ŀ����ͼ��ABCD��ƽ���ı��Σ�AB�ǡ�O��ֱ������D�ڡ�O�ϣ�AD��OA��2����ͼ����Ӱ���ֵ����Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
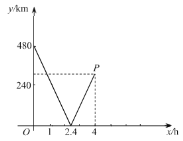
����Ŀ���ס�������֮����һ����ֱ�Ĺ�·���쳵�������ֱ�Ӽס�������ͬʱ��������������·����������У��쳵�����ҵغ�ֹͣ��ʻ����������غ�ֹͣ��ʻ����֪�쳵�ٶ�Ϊ![]() ����ͼΪ����֮��ľ���
����ͼΪ����֮��ľ���![]() ��������ʻʱ��
��������ʻʱ��![]() �IJ��ֺ���ͼ��
�IJ��ֺ���ͼ��
��1���ס�������֮��ľ�����______km��
��2����![]() ������Ϊ��4��____�������͵�
������Ϊ��4��____�������͵�![]() ��ʵ�����壮
��ʵ�����壮
��3���������⣬��ȫ����ͼ������Ҫ�����ݣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܡ��¹ڡ������Ӱ�죬ij����������������![]() ��
��![]() �����ͺŵġ���д�塱�������ķᣮ��֪
�����ͺŵġ���д�塱�������ķᣮ��֪![]() �ͣ�
�ͣ�![]() ����д����ۡ��ۼۺ�ÿ�������������ʾ��
����д����ۡ��ۼۺ�ÿ�������������ʾ��
���ۣ�Ԫ/���� | �ۼۣ�Ԫ/���� | ��������/�գ� | |
|
|
|
|
|
|
|
|
�����г����飬�������̶�![]() ����д�彵�����ۣ�ͬʱ��
����д�彵�����ۣ�ͬʱ��![]() ����д������ۼۣ���ʱ����
����д������ۼۣ���ʱ����![]() ����д��ÿ����
����д��ÿ����![]() Ԫ�Ϳɶ���
Ԫ�Ϳɶ���![]() ����
����![]() ����д��ÿ���
����д��ÿ���![]() Ԫ������
Ԫ������![]() ����Ҫ����ÿ�������������䣬������
����Ҫ����ÿ�������������䣬������![]() ����д��ÿ�������
����д��ÿ�������![]() ����ÿ���ܻ���������Ϊ
����ÿ���ܻ���������Ϊ![]() Ԫ
Ԫ
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��д��
֮��ĺ�����ϵʽ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��Ҫʹÿ���������![]() Ԫ��ֱ��д��
Ԫ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���������̾���ÿ����һ��![]() ����д�壬�;�
����д�壬�;�![]() Ԫ��
Ԫ��![]() ���¹����顱Ӱ������Ѽ�ͥ����
���¹����顱Ӱ������Ѽ�ͥ����![]() ʱ��ÿ����������Ϊ
ʱ��ÿ����������Ϊ![]() Ԫ����
Ԫ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������ס���������Ʒ��8���������һ��һ·�����߹��Һ͵�������֪2��������Ʒ��3��������Ʒ�����۶���ͬ��3��������Ʒ��2��������Ʒ�����۶��1500Ԫ��
��1��������Ʒ��������Ʒ�����۵��۸�����Ԫ��
��2�����ס���������Ʒ�������ܶ����5400��Ԫ�����������ۼ�����Ʒ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��Ϊ������ȫ�������������ƺţ���ĩ����ί��֯־Ը�߽��������.����������ʦ������4��Ů��ɲ���С�á�С�ݡ�С��Сٻ����ͨ����ǩ�ķ�ʽȷ��2��Ů��ȥ�μ�.
��ǩ����4��Ů��ɲ������ֱ�д��4����ȫ��ͬ�Ŀ�Ƭ���棬�����ſ�Ƭ���泯�ϣ�ϴ�Ⱥ���������ϣ�����ʦ�ȴ��������ȡһ�ſ�Ƭ�������������ٴ�ʣ���3�ſ�Ƭ�������ȡ�ڶ��ţ���������.
��1���ð�������С�ձ��������� �¼�����С�ñ��������� �¼�(������������������Ȼ�����������)����һ�γ�ȡ��Ƭ��С�ñ��������ĸ���Ϊ ��
��2�����û���״ͼ���б��ķ�����ʾ��γ�ǩ���п��ܵĽ�����������С�ݱ��������ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com