
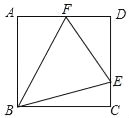
【题目】如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB的值是_____.
【答案】3
【解析】
根据正方形的性质得BA=BC,∠ABC=90°,则可把△BAE绕点B顺时针旋转90°得到△BCG,如图,根据旋转的性质得∠BCG=∠BAF=90°,∠FBG=∠ABC=90°,AF=CG,所以点G、C、F共线,再利用“SAS”证明△BFE≌△BGE,得到∠FEB=∠GEB,设正方形的边长为2a,CE=x,则AF=DF=a,CG=AF=a,DF=2a﹣x,EF=EG=x+a,在Rt△DEF中,利用勾股定理得到a2+(2a﹣x)2=(x+a)2,解得x=![]() a,然后在Rt△BCF中,根据正切的定义得tan∠BEC=
a,然后在Rt△BCF中,根据正切的定义得tan∠BEC=![]() =3,即tan∠FEB的值为3.
=3,即tan∠FEB的值为3.
∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
把△BAF绕点B顺时针旋转90°得到△BCG,如图,
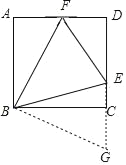
∴∠BCG=∠BAF=90°,∠FBG=∠ABC=90°,AF=CG,
∴点G、C、E共线,
∵∠EBF=45°,
∴∠GBE=45°,BG=BF,
在△BEF和△BGE中,
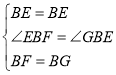 ,
,
∴△BEF≌△BGE(SAS),
∴∠FEB=∠GEB,
设正方形的边长为2a,CE=x,则AF=DF=a,CG=AF=a,DF=2a﹣x,EF=EG=x+a,
在Rt△DEF中,∵DF2+DE2=EF2,
∴a2+(2a﹣x)2=(x+a)2,
解得x=![]() a,
a,
在Rt△BCE中,
tan∠CEB=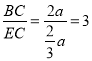 ,
,
∴tan∠FEB=3.
故答案为3.


科目:初中数学 来源: 题型:
【题目】(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
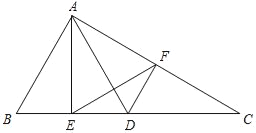
【题目】如图,在△ABC中,点D为边BC上一点,且AD=AB,AE⊥BC,垂足为点E.过点D作DF∥AB,交边AC于点F,连接EF,EF2=![]() BDEC.
BDEC.
(1)求证:△EDF∽△EFC;
(2)如果![]() ,求证:AB=BD.
,求证:AB=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家健身俱乐部收费标准为180元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次收费(元) |
A类 | 1500 | 100 |
B类 | 3000 | 60 |
C类 | 4000 | 40 |
例如,购买A类会员年卡,一年内健身20次,消费![]() 元,若一年内在该健身俱乐部健身的次数介于50-60次之间,则最省钱的方式为( )
元,若一年内在该健身俱乐部健身的次数介于50-60次之间,则最省钱的方式为( )
A.购买A类会员年卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
查看答案和解析>>
科目:初中数学 来源: 题型:
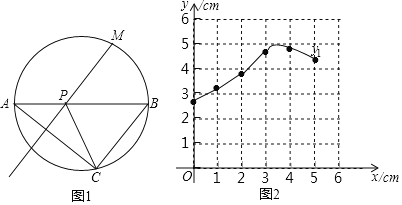
【题目】如图1,M是圆中![]() 上一定点,P是弦AB上一动点,过点A作射线MP的垂线交圆于点C,连接PC.已知AB=5cm,设A、P两点间的距离为xcm,A、C两点间的距离为y1cm,P、C两点的距离为y2cm.小帅根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.
上一定点,P是弦AB上一动点,过点A作射线MP的垂线交圆于点C,连接PC.已知AB=5cm,设A、P两点间的距离为xcm,A、C两点间的距离为y1cm,P、C两点的距离为y2cm.小帅根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.
下面是小帅的探究过程,请补充完整:
(1)按照表中自变量x的值进行取点,画图、测量,分别得到了y1、y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y1/cm | 2.55 | 3.15 | 3.95 | 4.76 | 4.95 | 4.30 |
y2/cm | 2.55 | 2.64 | 2.67 |
| 1.13 | 2.55 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:在点P的运动过程中,当AC与PC的差为最大值时,AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
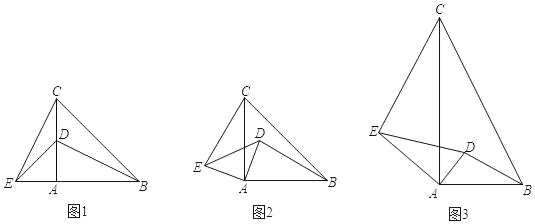
问题情境:如图1,在数学活动课上,老师让同学们画了等腰Rt△ABC和等腰Rt△ADE,并连接CE,BD.
操作发现:(1)当等腰Rt△ADE绕点A旋转,如图2,勤奋小组发现了:
①线段CE与线段BD之间的数量关系是 .
②直线CE与直线BD之间的位置关系是 .
类比思考:(2)智慧小组在此基础上进行了深入思考,如图3,若△ABC与△ADE都为直角三角形,∠BAC=∠DAE=90°,且AC=2AB,AE=2AD,请你写出CE与BD的数量关系和位置关系,并加以证明.
拓展应用:(3)创新小组在(2)的基础上,又作了进一步拓展研究,当点E在直线AB上方时,若DE∥AB,且AB=![]() ,AD=1,其他条件不变,试求出线段CE的长.(直接写出结论)
,AD=1,其他条件不变,试求出线段CE的长.(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
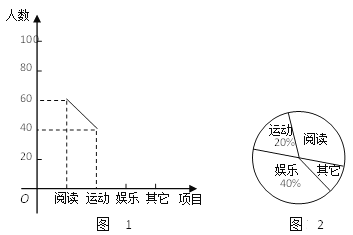
【题目】某中学团委会为研究该校学生的课余活动情况,采取抽样的方法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图(如图1,图2),请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了多少名学生?
(2)“其它”在扇形图中所占的圆心角是多少度?
(3)补全频数分布折线图.
查看答案和解析>>
科目:初中数学 来源: 题型:
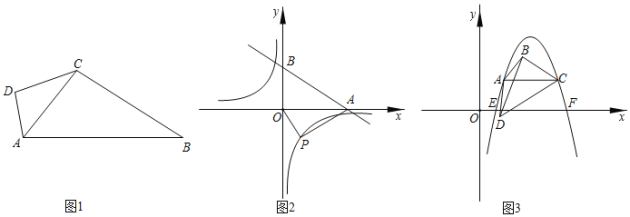
【题目】四边形的一条对角线将这个四边形分成两个三角形,如果这两个三角形相似(不全等),那么我们将这条对角线叫做这个四边形的相似对角线.
(1)如图1,四边形ABCD中,∠DAB=100°,∠DCB=130°,对角线AC平分∠DAB,求证:AC是四边形ABCD的相似对角线;
(2)如图2,直线![]() 分别与x,y轴相交于A,B两点,P为反比例函数y=
分别与x,y轴相交于A,B两点,P为反比例函数y=![]() (k<0)上的点,若AO是四边形ABOP的相似对角线,求反比例函数的解析式;
(k<0)上的点,若AO是四边形ABOP的相似对角线,求反比例函数的解析式;
(3)如图3,AC是四边形ABCD的相似对角线,点C的坐标为(3,1),AC∥x轴,∠BCA=∠DCA=30°,连接BD,△BCD的面积为![]() .过A,C两点的抛物线y=ax2+bx+c(a<0)与x轴交于E,F两点,记|m|=AC+1,若直线y=mx与抛物线恰好有3个交点,求实数a的值.
.过A,C两点的抛物线y=ax2+bx+c(a<0)与x轴交于E,F两点,记|m|=AC+1,若直线y=mx与抛物线恰好有3个交点,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 、
、![]() 、
、![]() 三点的坐标分别为
三点的坐标分别为![]() ,
,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,连接
上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 从
从![]() 运动到
运动到![]() 时,点
时,点![]() 随之运动,设点
随之运动,设点![]() 的坐标为
的坐标为![]() ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com