
【题目】综合与实践
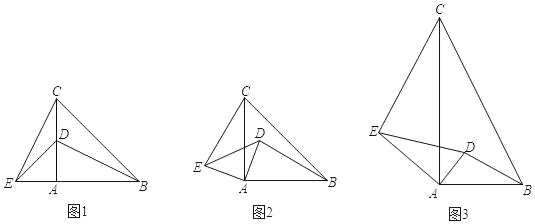
问题情境:如图1,在数学活动课上,老师让同学们画了等腰Rt△ABC和等腰Rt△ADE,并连接CE,BD.
操作发现:(1)当等腰Rt△ADE绕点A旋转,如图2,勤奋小组发现了:
①线段CE与线段BD之间的数量关系是 .
②直线CE与直线BD之间的位置关系是 .
类比思考:(2)智慧小组在此基础上进行了深入思考,如图3,若△ABC与△ADE都为直角三角形,∠BAC=∠DAE=90°,且AC=2AB,AE=2AD,请你写出CE与BD的数量关系和位置关系,并加以证明.
拓展应用:(3)创新小组在(2)的基础上,又作了进一步拓展研究,当点E在直线AB上方时,若DE∥AB,且AB=![]() ,AD=1,其他条件不变,试求出线段CE的长.(直接写出结论)
,AD=1,其他条件不变,试求出线段CE的长.(直接写出结论)
【答案】(1)EC=BD; BD⊥EC;(2) CE=2BD,CE⊥BD.理由见解析;(3)4.
【解析】
(1)如图2中,延长BD交AC于点O,交EC于H.证明△EAC≌△DAB(SAS),即可解决问题.
(2)结论:CE=2BD,CE⊥BD.如图3中,延长BD交AC于点O,交EC于点H.证明△ABD∽△ACE,即可解决问题.
(3)如图4中,当DE∥AB时,设DE交AC于H,易证AC⊥DE.求出EH,CH,理由勾股定理即可解决问题.
(1)如图2中,延长BD交AC于点O,交EC于H.
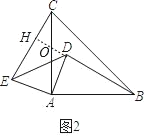
∵AE=AD,AC=AB,∠EAD=∠CAB=90°,
∴∠EAC=∠DAB,
∴△EAC≌△DAB(SAS),
∴EC=BD,∠ECA=∠ABD,
∵∠ABD+∠AOB=90°,∠AOB=∠COH,
∴∠ECA+∠COH=90°,
∴∠CHO=90°,
∴BD⊥EC,
故答案为EC=BD,BD⊥EC.
(2)结论:CE=2BD,CE⊥BD.
理由:如图3中,延长BD交AC于点O,交EC于点H.

∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵AC=2AB,AE=2AD,
∴![]() ,
,
∴△ABD∽△ACE,
∴![]() ,
,
∴CE=2BD,∠ABD=∠ACE,
∵∠ABD+∠AOB=90°,∠AOB=∠COH,
∴∠ECA+∠COH=90°,
∴∠CHO=90°,
∴BD⊥EC.
(3)如图4中,当DE∥AB时,设DE交AC于H,易证AC⊥DE.

∵AE=2AD,AD=1,
∴AE=2,DE=![]() ,
,![]() ,
,![]() ,
,
∵AC=2AB,AB=![]() ,
,
∴CH=AC﹣AH=![]() ,
,
在Rt△ECH中,EC=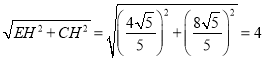 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家,爱园艺”、
.“爱我家,爱园艺”、![]() .“园艺小清新之旅”和
.“园艺小清新之旅”和![]() .“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
.“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李欣选择线路![]() .“园艺小清新之旅”的概率是多少?
.“园艺小清新之旅”的概率是多少?
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一线路游览的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,P是BA延长线上一点,过点P作⊙O的切线,切点为D,连接BD,过点B作射线PD的垂线,垂足为C.

(1)求证:BD平分∠ABC;
(2)如果AB=6,sin∠CBD![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接国庆节,某工厂生产一种火爆的纪念商品,每件商品成本25元,工厂将该商品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.

(1)求![]() 与
与![]() 的函数解析式(也称关系式).
的函数解析式(也称关系式).
(2)若一次性批发量超过20且不超过50件时,求获得的利润![]() 与
与![]() 的函数关系式,同时求当批发量为多少件时,工厂获利最大?最大利润是多少?
的函数关系式,同时求当批发量为多少件时,工厂获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
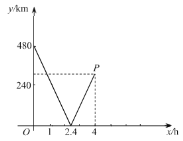
【题目】甲、乙两地之间有一条笔直的公路,快车和慢车分别从甲、乙两地同时出发,沿这条公路匀速相向而行,快车到达乙地后停止行驶,慢车到达甲地后停止行驶,已知快车速度为![]() .下图为两车之间的距离
.下图为两车之间的距离![]() 与慢车行驶时间
与慢车行驶时间![]() 的部分函数图像.
的部分函数图像.
(1)甲、乙两地之间的距离是______km;
(2)点![]() 的坐标为(4,____),解释点
的坐标为(4,____),解释点![]() 的实际意义.
的实际意义.
(3)根据题意,补全函数图像(标明必要的数据).
查看答案和解析>>
科目:初中数学 来源: 题型:
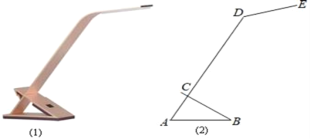
【题目】如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)
(1)求DE与水平桌面(AB所在直线)所成的角;
(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com