
”¾ĢāÄæ”æĪäŗŗŹŠĪķö²ĢģĘųŃĻÖŲ£¬»·¾³ÖĪĄķŅŃæĢ²»ČŻ»ŗ£¬ĪäŗŗŹŠÄ³µēĘ÷ÉĢ³”øł¾ŻĆńÖŚ½”浊čŅŖ£¬“śĄķĻśŹŪijÖÖ¼ŅÓĆæÕĘų¾»»ÆĘ÷£¬Ęä½ų¼ŪŹĒ200ŌŖ/ĢØ£¬¾¹żŹŠ³”ĻśŹŪŗó·¢ĻÖ£ŗŌŚŅ»øöŌĀÄŚ£¬µ±ŹŪ¼ŪŹĒ400ŌŖ/ĢØŹ±£¬æÉŹŪ³ö200ĢØ£¬ĒŅŹŪ¼ŪĆæ½µµĶ10ŌŖ£¬¾ĶæɶąŹŪ³ö50ĢØ£¬Čō¹©Ó¦ÉĢ¹ę¶ØÕāÖÖæÕĘų¾»»ÆĘ÷ŹŪ¼Ū²»µĶÓŚ330ŌŖ/ĢØ£¬“śĄķĻśŹŪÉĢĆæŌĀŅŖĶź³É²»µĶÓŚ450ĢصÄĻśŹŪČĪĪń£®
£Ø1£©ŹŌČ·¶ØŌĀĻśŹŪĮæ![]() £ØĢØ£©ÓėŹŪ¼Ū
£ØĢØ£©ÓėŹŪ¼Ū![]() £ØŌŖ/ĢØ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£ØŌŖ/ĢØ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø2£©µ±ŹŪ¼Ū![]() £ØŌŖ/ĢØ£©¶ØĪŖ¶ąÉŁŹ±£¬ÉĢ³”ĆæŌĀĻśŹŪÕāÖÖæÕĘų¾»»ÆĘ÷Ėł»ńµĆµÄĄūČó
£ØŌŖ/ĢØ£©¶ØĪŖ¶ąÉŁŹ±£¬ÉĢ³”ĆæŌĀĻśŹŪÕāÖÖæÕĘų¾»»ÆĘ÷Ėł»ńµĆµÄĄūČó![]() £ØŌŖ£©×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
£ØŌŖ£©×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
£Ø3£©µ±ŹŪ¼Ū![]() £ØŌŖ/ĢØ£©Āś×ćŹ²Ć“Ģõ¼žŹ±£¬ÉĢ³”ĆæŌĀĻśŹŪÕāÖÖæÕĘų¾»»ÆĘ÷Ėł»ńµĆµÄĄūČó
£ØŌŖ/ĢØ£©Āś×ćŹ²Ć“Ģõ¼žŹ±£¬ÉĢ³”ĆæŌĀĻśŹŪÕāÖÖæÕĘų¾»»ÆĘ÷Ėł»ńµĆµÄĄūČó![]() £ØŌŖ£©²»µĶÓŚ70000ŌŖ£æ
£ØŌŖ£©²»µĶÓŚ70000ŌŖ£æ
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©µ±ŹŪ¼ŪĪŖ330ŌŖ/ĢØŹ±£¬ŌĀĄūČó×ī“óĪŖ71500ŌŖ£»£Ø3£©
£»£Ø2£©µ±ŹŪ¼ŪĪŖ330ŌŖ/ĢØŹ±£¬ŌĀĄūČó×ī“óĪŖ71500ŌŖ£»£Ø3£©![]() Ź±£¬ÉĢ³”ĆæŌĀĻśŹŪÕāÖÖæÕĘų¾»»ÆĘ÷Ėł»ńµĆµÄĄūČó²»µĶÓŚ70000ŌŖ£®
Ź±£¬ÉĢ³”ĆæŌĀĻśŹŪÕāÖÖæÕĘų¾»»ÆĘ÷Ėł»ńµĆµÄĄūČó²»µĶÓŚ70000ŌŖ£®
”¾½āĪö”æ
£Ø1£©øł¾ŻĻśŹŪĮæ=ŌĄ“µÄĻśŹŪĮæ+½µ¼ŪŗóµÄĻśŹŪĮæ¾ĶæÉŅŌ±ķŹ¾³öyÓėxÖ®¼äµÄ¹ŲĻµŹ½£»
£Ø2£©ÓÉ×ÜĄūČó=ĆæĢØµÄĄūČó”ĮŹżĮæ¾ĶæÉŅŌµĆ³öWÓėxÖ±½ÓµÄ¹ŲĻµŹ½£¬Óɶž“ĪŗÆŹżµÄŠŌÖŹ¾ĶæÉŅŌµĆ³ö½įĀŪ£»
£Ø3£©µ±W=70000Ź±£¬“śČė£Ø2£©µÄ½āĪöŹ½Ēó³öxµÄÖµ£¬Óɶž“ĪŗÆŹżµÄ¶ųĻÖŌŚ¾ĶæÉŅŌĒó³ö½įĀŪ£®
½ā£ŗ£Ø1£©ÓÉĢāŅā£¬µĆ![]() £¬
£¬
![]() £®
£®
“š£ŗ![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ![]() £»
£»
£Ø2£©ÓÉĢāŅā£¬µĆ£ŗ
![]() £¬
£¬
![]() £¬
£¬
”ߏŪ¼Ū²»µĶÓŚ330ŌŖ/ĢØ £¬
”ą![]()
”ߏżĮæ²»µĶÓŚ450ŌŖ £¬
”ą![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬
”ąŌŚ¶Ō³ĘÖįµÄÓŅ²ą![]() Ėę
Ėę![]() µÄŌö“ó¶ų¼õŠ”£¬
µÄŌö“ó¶ų¼õŠ”£¬
”ą![]() Ź±£¬
Ź±£¬![]() ×ī“ó=71500£®
×ī“ó=71500£®
“š£ŗµ±ŹŪ¼ŪĪŖ330ŌŖ/ĢØŹ±£¬ŌĀĄūČó×ī“óĪŖ71500ŌŖ£®
£Ø3£©ÓÉĢāŅā£¬µĆ![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() Ź±£¬ÉĢ³”ĆæŌĀĻśŹŪÕāÖÖæÕĘų¾»»ÆĘ÷Ėł»ńµĆµÄĄūČó²»µĶÓŚ70000ŌŖ.
Ź±£¬ÉĢ³”ĆæŌĀĻśŹŪÕāÖÖæÕĘų¾»»ÆĘ÷Ėł»ńµĆµÄĄūČó²»µĶÓŚ70000ŌŖ.


 æŖŠÄæģĄÖ¼ŁĘŚ×÷ŅµŹī¼Ł×÷ŅµĪ÷°²³ö°ęÉēĻµĮŠ“š°ø
æŖŠÄæģĄÖ¼ŁĘŚ×÷ŅµŹī¼Ł×÷ŅµĪ÷°²³ö°ęÉēĻµĮŠ“š°ø ĆūĢāѵĮ·ĻµĮŠ“š°ø
ĆūĢāѵĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ ČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬FĪŖĻŅACµÄÖŠµć£¬Į¬½ÓOF²¢ŃÓ³¤½»»”ACÓŚµćD£¬¹żµćD×÷”ŃOµÄĒŠĻߣ¬½»BAµÄŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓCD£¬OC£®
£Ø1£©ĒóÖ¤£ŗAC”ĪDE£»
£Ø2£©ČōOA=AE£¬ĒóÖ¤£ŗ”÷AFO”Õ”÷CFD£»
£Ø3£©ČōOA=AE=2£¬ŌņĖıߊĪACDEµÄĆ껿ŹĒ______£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«Ņ»ÕÅĆ껿ĪŖ![]() µÄ“óČż½ĒŠĪÖ½Ę¬ŃŲ×ÅŠéĻß¼ō³ÉČżÕÅŠ”Čż½ĒŠĪÖ½Ę¬ÓėŅ»ÕÅĘ½ŠŠĖıߊĪÖ½Ę¬£® øł¾ŻĶ¼ÖŠ±źŹ¾µÄ³¤¶Č£¬Ę½ŠŠĖıߊĪÖ½Ę¬µÄĆ껿ĪŖ£Ø £©
µÄ“óČż½ĒŠĪÖ½Ę¬ŃŲ×ÅŠéĻß¼ō³ÉČżÕÅŠ”Čż½ĒŠĪÖ½Ę¬ÓėŅ»ÕÅĘ½ŠŠĖıߊĪÖ½Ę¬£® øł¾ŻĶ¼ÖŠ±źŹ¾µÄ³¤¶Č£¬Ę½ŠŠĖıߊĪÖ½Ę¬µÄĆ껿ĪŖ£Ø £©
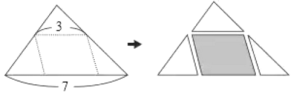
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
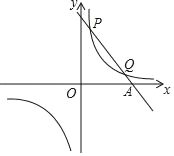
”¾ĢāÄæ”æŅŃÖŖŅ»“ĪŗÆŹży£½k1x+bÓė·“±ČĄżŗÆŹży£½![]() µÄĶ¼Ļó½»ÓŚµŚŅ»ĻóĻŽÄŚµÄP£Ø
µÄĶ¼Ļó½»ÓŚµŚŅ»ĻóĻŽÄŚµÄP£Ø![]() £¬8£©£¬Q£Ø4£¬m£©Į½µć£¬ÓėxÖį½»ÓŚAµć£®
£¬8£©£¬Q£Ø4£¬m£©Į½µć£¬ÓėxÖį½»ÓŚAµć£®
£Ø1£©Š“³öµćP¹ŲÓŚŌµćµÄ¶Ō³ĘµćP”äµÄ×ų±ź£»
£Ø2£©·Ö±šĒó³öÕāĮ½øöŗÆŹżµÄ±ķ“ļŹ½£»
£Ø3£©Ēó”ĻP”äAOµÄÕżĒŠÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() ĪŖ”Ń
ĪŖ”Ń![]() µÄÖ±¾¶£¬
µÄÖ±¾¶£¬![]() ŹĒ”Ń
ŹĒ”Ń![]() ÉĻµÄĮ½µć£¬¹ż
ÉĻµÄĮ½µć£¬¹ż![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬¹ż
£¬¹ż![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬
£¬![]() ĪŖ
ĪŖ![]() ÉĻµÄČĪŅāŅ»µć£¬Čō
ÉĻµÄČĪŅāŅ»µć£¬Čō![]() £¬
£¬![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() µÄ×īŠ”ÖµŹĒ__________£®
µÄ×īŠ”ÖµŹĒ__________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
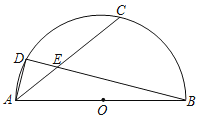
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ°ėŌ²OµÄÖ±¾¶£¬DŹĒ°ėŌ²OÉĻŅ»µć£¬CŹĒ![]() µÄÖŠµć£¬Į¬½įAC½»BDÓŚµćE£¬Į¬½įAD£¬ČōBE£½4DE£¬CE£½6£¬ŌņABµÄ³¤ĪŖ_____£®
µÄÖŠµć£¬Į¬½įAC½»BDÓŚµćE£¬Į¬½įAD£¬ČōBE£½4DE£¬CE£½6£¬ŌņABµÄ³¤ĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßy£½©![]() x2+bx+cÓėxÖį½»ÓŚµćA£Ø©3£¬0£©ŗĶµćB£¬ÓėyÖį½»ÓŚµćC £Ø0£¬2£©£®
x2+bx+cÓėxÖį½»ÓŚµćA£Ø©3£¬0£©ŗĶµćB£¬ÓėyÖį½»ÓŚµćC £Ø0£¬2£©£®
£Ø1£©ĒóÅ×ĪļĻߵıķ“ļŹ½£¬²¢ÓĆÅä·½·ØĒó³ö¶„µćDµÄ×ų±ź£»
£Ø2£©ČōµćEŹĒµćC¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖįµÄ¶Ō³Ęµć£¬Ēótan”ĻCEBµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
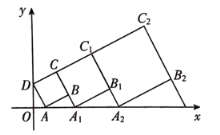
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Õż·½ŠĪABCD µÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬µćAµÄ×ų±źĪŖ£Ø1£¬0£©£¬µćDµÄ×ų±źĪŖ£Ø0£¬2£©£¬ŃÓ³¤CB½»xÖįÓŚµćA1£¬×÷Õż·½ŠĪA1CC1B1£¬ŃÓ³¤C1B1½»xÖįÓŚµćA2£¬×÷Õż·½ŠĪA2C1C2B2£¬”£¬°“ÕÕÕāŃłµÄ¹ęĀÉ×÷Õż·½ŠĪ£¬ŌņµćB2019µÄׯ×ų±źĪŖ_______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģx2+mx©6£½0£®
£Ø1£©ĒóÖ¤£ŗ²»ĀŪmĪŖŗĪŹµŹż£¬·½³Ģ×ÜÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£»
£Ø2£©Čōm£½1£¬ÓĆÅä·½·Ø½āÕāøöŅ»ŌŖ¶ž“Ī·½³Ģ£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com