
【题目】如图,将一张面积为![]() 的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片. 根据图中标示的长度,平行四边形纸片的面积为( )
的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片. 根据图中标示的长度,平行四边形纸片的面积为( )
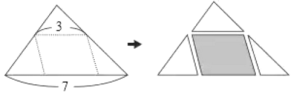
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
设△ADE,△BDF,△CEG,平行四边形DEGF的面积分别为S1,S2,S3和S,过点D作DH∥EC,由DFGE为平行四边形,易得四边形DHCE也为平行四边形,从而△DFH≌△EGC,易得△ADE∽△ABC,得![]() ,结合S△BDH=
,结合S△BDH=![]() S,列出关于S的方程,即可求解.
S,列出关于S的方程,即可求解.
设△ADE,△BDF,△CEG,平行四边形DEGF的面积分别为S1,S2,S3和S,过点D作DH∥EC,
∵四边形DFGE为平行四边形,
∴DE∥HC,
∴四边形DHCE为平行四边形,
∴DH=EC,
∵DH∥EC,
∴∠DHF=∠ECG,
∵DF∥EG,
∴∠DFH=∠EGC,
∴△DFH≌△EGC(AAS),
∴S△DFH=S3,
∵DE∥BC,
∴△ADE∽△ABC,
∵DE=3,BC=7,
∴![]() ,
,
∵S△ABC=14,
∴![]() ,
,
∵BH=BC-CH=7-3=4,FG=DE=3,
∴S△BDH:S=(![]() ×4):3=2:3,
×4):3=2:3,
∴S△BDH=![]() S,
S,
∴![]() ,
,
∴S=![]() .
.
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
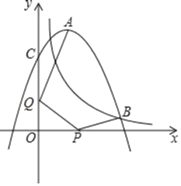
【题目】如图,抛物线y=ax2+4x+c(a≠0)与反比例函数y=![]() 的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
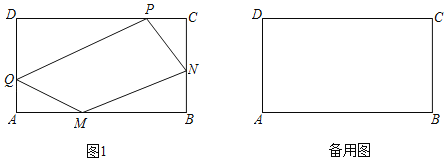
【题目】如图1,点M,N,P,Q分别在矩形ABCD的边AB,BC,CD,DA上,我们称四边形MNPQ是矩形ABCD的内接四边形.已知矩形ABCD,AB=2BC=6,若它的内接四边形MNPQ也是矩形,且相邻两边的比为3:1,则AM=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络购物已成为新的消费方式,催生了快递行业的高速发展,某小型的快递公司,今年5月份与7月份完成快递件数分别为5万件和5.832份万件,假定每月投递的快递件数的增长率相同.
(1)求该快递公司投递的快递件数的月平均增长率;
(2)如果每个快递小哥平均每月最多可投递0.8万件,公司现有8个快递小哥,按此快递增长速度,不增加人手的情况下,能否完成今年9月份的投递任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉嘉和淇淇做一个游戏,他们拿出![]() 张扑克牌,将数字为
张扑克牌,将数字为![]() 的四张牌给嘉嘉,将数字为
的四张牌给嘉嘉,将数字为![]() 的四张牌给淇淇,再从各自的四张牌中随机抽出一张.
的四张牌给淇淇,再从各自的四张牌中随机抽出一张.
(1)用列表法或树状图表示出所得数字的所有情况;
(2)如果比大小,谁抽出的数字大谁获胜,嘉嘉获胜的概率是多少?
(3)如果求和,抽出的两个数字和为奇数,嘉嘉获胜;和为偶数,淇淇获胜,谁获胜的概率大,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
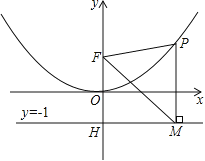
【题目】二次函数图象的顶点在原点O,经过点A(1,![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉市雾霾天气严重,环境治理已刻不容缓,武汉市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台,经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台,若供应商规定这种空气净化器售价不低于330元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量![]() (台)与售价
(台)与售价![]() (元/台)之间的函数关系式.
(元/台)之间的函数关系式.
(2)当售价![]() (元/台)定为多少时,商场每月销售这种空气净化器所获得的利润
(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
(3)当售价![]() (元/台)满足什么条件时,商场每月销售这种空气净化器所获得的利润
(元/台)满足什么条件时,商场每月销售这种空气净化器所获得的利润![]() (元)不低于70000元?
(元)不低于70000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
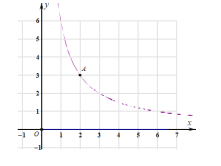
【题目】如图,在平面直角坐标系 xOy中,反比例函数 y ![]() x 0 的图象经过点 A2,3 ,直线y ax , y
x 0 的图象经过点 A2,3 ,直线y ax , y ![]() 与反比例函数 y
与反比例函数 y ![]() x 0 分别交于点 B,C两点.
x 0 分别交于点 B,C两点.
(1)直接写出 k 的值 ;
(2)由线段 OB,OC和函数 y ![]() x 0 在 B,C 之间的部分围成的区域(不含边界)为 W.
x 0 在 B,C 之间的部分围成的区域(不含边界)为 W.
① 当 A点与 B点重合时,直接写出区域 W 内的整点个数 ;
② 若区域 W内恰有 8个整点,结合函数图象,直接写出 a的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com