
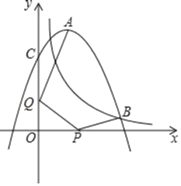
【题目】如图,抛物线y=ax2+4x+c(a≠0)与反比例函数y=![]() 的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
【答案】![]()
【解析】
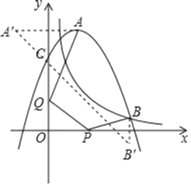
根据题意求得B的坐标,然后根据待定系数法求得抛物线的解析式,从而求得顶点A的坐标,求得A关于y轴的对称点A′(-2,10),B点关于x轴的对称点B′为(5,-1),根据两点之间线段最短,即可判断AQ+QP+PB=A′B′是AQ+QP+PB的最小值,利用勾股定理求得即可.
∵点B在反比例函数y=![]() 的图象,且点B的横坐标为5,
的图象,且点B的横坐标为5,
∴点B的纵坐标为:y=![]() =1,
=1,
∴B(5,1),
∵抛物线y=ax2+4x+c(a≠0)与反比例函数y=![]() 的图象相交于点B,与y轴交于点C(0,6),
的图象相交于点B,与y轴交于点C(0,6),
∴![]() ,解得
,解得![]() ,
,
∴抛物线为y=﹣x2+4x+6,
∵y=﹣x2+4x+6=﹣(x﹣2)2+10,
∴A(2,10),
∴A关于y轴的对称点A′(﹣2,10),
∵B(5,1),
∴B点关于x轴的对称点B′为(5,﹣1),
连接A′B′交x轴于P,交y轴于Q,此时AQ+QP+PB的值最小,即AQ+QP+PB=A′B′,
A′B′=![]() =
=![]() ,
,
故AQ+QP+PB的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,顶点为(1,4)的抛物线![]() 与直线
与直线![]() 交于点A(2,2),直线
交于点A(2,2),直线![]() 与
与![]() 轴交于点B与
轴交于点B与![]() 轴交于点C
轴交于点C
(1)求![]() 的值及抛物线的解析式
的值及抛物线的解析式
(2)P为抛物线上的点,点P关于直线AB的对称轴点在![]() 轴上,求点P的坐标
轴上,求点P的坐标
(3)点D为![]() 轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
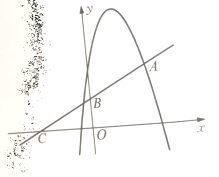
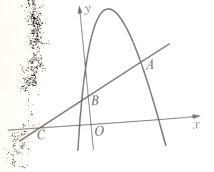
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.25人中至少有3人的出生月份相同
B.任意抛掷一枚均匀的1元硬币,若上一次正面朝上,则下一次一定反面朝上
C.天气预报说明天降雨的概率为10%,则明天一定是晴天
D.任意抛掷一枚均匀的骰子,掷出的点数小于3的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016青海省西宁市)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
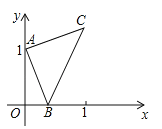
A. B.
B.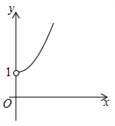 C.
C.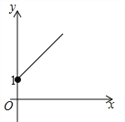 D.
D.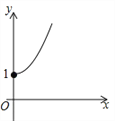
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E,连接CD,OC.
(1)求证:AC∥DE;
(2)若OA=AE,求证:△AFO≌△CFD;
(3)若OA=AE=2,则四边形ACDE的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
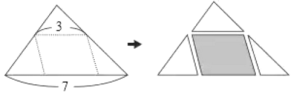
【题目】如图,将一张面积为![]() 的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片. 根据图中标示的长度,平行四边形纸片的面积为( )
的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片. 根据图中标示的长度,平行四边形纸片的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com