
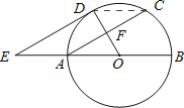
【题目】 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E,连接CD,OC.
(1)求证:AC∥DE;
(2)若OA=AE,求证:△AFO≌△CFD;
(3)若OA=AE=2,则四边形ACDE的面积是______.

【答案】(1)详见解析;(2)详见解析;(3)2![]() .
.
【解析】
(1)先根据切线的性质得出OD⊥DE,再根据垂定定理得出OD⊥AC,即可得出结论;
(2)先判断出OE=2OD,进而得出∠E=30°,进而得出∠C=30°=∠OAF,即可用ASA判断出△AFO≌△CFD;
(3)先求出△ODE的面积,再根据(2)△AFO≌△CFD,得出S△AFO=S△CFD,即可得出结论.
(1)证明:∵DE是⊙O的切线,
∴OD⊥DE,
∵F为⊙O中弦AC的中点,
∴OD⊥AC,
∴AC∥DE;
(2)解:如图,
连接CD,由(1)知,OD⊥DE,
∴∠ODE=90°,
∵OA=AE,
∴OE=AE+OA=2OA,
∵OA=OD,
∴OE=2OD,
在Rt△ODE中,OE=2OD,
∴∠E=30°,
∴∠DOE=90°-30°=60°,
∴∠C=![]() ∠AOD=30°,
∠AOD=30°,
由(1)知,AC∥DE,
∴∠OAF=∠E=30°=∠C,
∵点F是AC的中点,
∴AF=CF,
由(1)知,OD⊥AC,
∴∠AFO=∠CFD=90°,
在△AFO和△CFD中,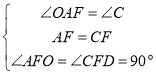
∴△AFO≌△CFD(ASA);
(3)∵OA=AE=2,
∴OE=OA+AE=4,OD=OA=2,
根据勾股定理得,DE=![]() =
=![]() =2
=2![]() ,
,
∴S△ODE=![]() ODDE=
ODDE=![]() ×2×2
×2×2![]() =2
=2![]()
由(2)知,△AFO≌△CFD,
∴S△AFO=S△CFD,
∴S四边形ACDE=S四边形DEAF+S△CFD=S四边形DEAF+S△AFO=S△ODE=2![]() ,
,
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
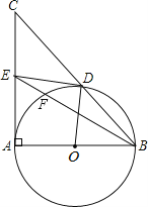
【题目】如图,在△ABC中,∠BAC=90°,AB是⊙O的直径,⊙O交BC于点D,E为AC的中点,BE交⊙O于点F.
(1)求证:DE是⊙O的切线.
(2)①当∠B=______时,四边形AODE是正方形;
②在①的条件下,若OA=2,线段BF的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
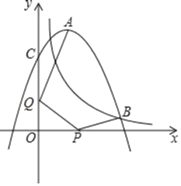
【题目】如图,抛物线y=ax2+4x+c(a≠0)与反比例函数y=![]() 的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与直线y=x﹣2交于点A(3,m).
(x>0)的图象与直线y=x﹣2交于点A(3,m).
(1)求k,m的值;
(2)已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x﹣2于点M,过点P作平行于x轴的直线交函数y=![]() (x>0)x的图象于点N.
(x>0)x的图象于点N.
①当n=3时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
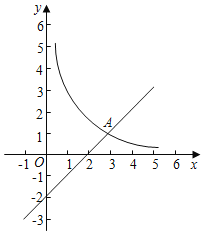
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四张质地均匀,大小完全相同的卡片,在其正面分别标有数字﹣1,﹣2,2,3,把卡片背面朝上洗匀,从中随机抽出一张后,不放回,再从中随机抽出一张,则两次抽出的卡片所标数字之和为正数的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南开封的西瓜个大瓤红且甜,全国知名![]() 某瓜农准备从某货运公司租用大小两种型号的货车运输西瓜到外地销售,已知一辆大型货车和一辆小型货车每次共运10吨;两辆大型货车和三辆小型渣货车每次共运24吨.
某瓜农准备从某货运公司租用大小两种型号的货车运输西瓜到外地销售,已知一辆大型货车和一辆小型货车每次共运10吨;两辆大型货车和三辆小型渣货车每次共运24吨.
![]() 求一辆大型货车和一辆小型货车每次各运西瓜多少吨?
求一辆大型货车和一辆小型货车每次各运西瓜多少吨?
![]() 已知一辆大型货车运输花费为400元
已知一辆大型货车运输花费为400元![]() 次,一辆小型货车运输花费为300元
次,一辆小型货车运输花费为300元![]() 次,计划用20辆货车运输,且每次运输西瓜总重量不少于96吨,如何安排才能使每次运费最低,最低费用是多少?
次,计划用20辆货车运输,且每次运输西瓜总重量不少于96吨,如何安排才能使每次运费最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
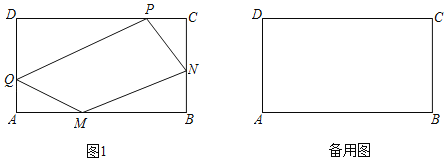
【题目】如图1,点M,N,P,Q分别在矩形ABCD的边AB,BC,CD,DA上,我们称四边形MNPQ是矩形ABCD的内接四边形.已知矩形ABCD,AB=2BC=6,若它的内接四边形MNPQ也是矩形,且相邻两边的比为3:1,则AM=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉市雾霾天气严重,环境治理已刻不容缓,武汉市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台,经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台,若供应商规定这种空气净化器售价不低于330元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量![]() (台)与售价
(台)与售价![]() (元/台)之间的函数关系式.
(元/台)之间的函数关系式.
(2)当售价![]() (元/台)定为多少时,商场每月销售这种空气净化器所获得的利润
(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
(3)当售价![]() (元/台)满足什么条件时,商场每月销售这种空气净化器所获得的利润
(元/台)满足什么条件时,商场每月销售这种空气净化器所获得的利润![]() (元)不低于70000元?
(元)不低于70000元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com