
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)如图2,当⊙P与边CD相切于点F时,求AP的长;
(2)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .

【答案】(1)AP=![]() ;(2)
;(2)![]() <AP<
<AP<![]() 或AP=5.
或AP=5.
【解析】
(1)如图2所示,连接PF,在Rt△ABC中,利用勾股定理求出AC=8,设AP=x,则DP=10﹣x,PF=x,由⊙P与边CD相切于点F,根据已知可推导得出△DPF∽△DAC,根据相似三角形对应边成比例即可求得AP长;
(2)当⊙P与BC相切时,设切点为G,如图3,利用面积法求出PG=![]() ,然后分两种情况①⊙P与边AD、CD分别有两个公共点,②⊙P过点A、C、D三点,分别讨论即可得.
,然后分两种情况①⊙P与边AD、CD分别有两个公共点,②⊙P过点A、C、D三点,分别讨论即可得.
(1)如图2所示,连接PF,
在Rt△ABC中,由勾股定理得:AC=![]() =8,
=8,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴![]() ,
,
∴![]() ,
,
∴x=![]() ,即AP=
,即AP=![]() ;
;
(2)当⊙P与BC相切时,设切点为G,如图3,
SABCD=![]() ×6×8×2=10PG,
×6×8×2=10PG,
PG=![]() ,
,
①当⊙P与边AD、CD分别有两个公共点时,![]() <AP<
<AP<![]() ,即此时⊙P与平行四边形ABCD的边的公共点的个数为4,
,即此时⊙P与平行四边形ABCD的边的公共点的个数为4,
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,
此时AP=5,
综上所述,AP的值的取值范围是:![]() <AP<
<AP<![]() 或AP=5.
或AP=5.
故答案为:![]() <AP<
<AP<![]() 或AP=5.
或AP=5.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG,BF⊥AG,垂足分别为点E,F.求证:![]() ;
;

(2)在图1的基础上,若过点C作CH⊥DE,垂足为点H,连接AH,CF,如图2.求证:四边形AFCH为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:

(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
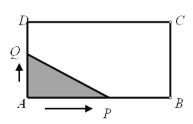
【题目】如图,长方形ABCD中,AB=4,AD=2.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为![]() (秒),在整个运动过程中,当△APQ为直角三角形时,则相应的
(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的![]() 的值或取值范围是_________.
的值或取值范围是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,校园内有两幢高度相同的教学楼AB,CD,大楼的底部B,D在同一平面上,两幢楼之间的距离BD长为24米,小明在点E(B,E,D在一条直线上)处测得教学楼AB顶部的仰角为45°,然后沿EB方向前进8米到达点G处,测得教学楼CD顶部的仰角为30°.已知小明的两个观测点F,H距离地面的高度均为1.6米,求教学楼AB的高度AB长.(精确到0.1米)参考值:![]() ≈1.41,
≈1.41,![]() ≈1.73.
≈1.73.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论:① △ODC是等边三角形;②BC=2AB;③∠AOE=135°; ④S△AOE=S△COE,其中正确的结论的个数有

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为6cm,点E,M分别是线段BD,AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图①,若点M与点D重合,求证:AF=MN;
(2)如图②,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以![]() cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.
①设BF=ycm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com