
【题目】如图,校园内有两幢高度相同的教学楼AB,CD,大楼的底部B,D在同一平面上,两幢楼之间的距离BD长为24米,小明在点E(B,E,D在一条直线上)处测得教学楼AB顶部的仰角为45°,然后沿EB方向前进8米到达点G处,测得教学楼CD顶部的仰角为30°.已知小明的两个观测点F,H距离地面的高度均为1.6米,求教学楼AB的高度AB长.(精确到0.1米)参考值:![]() ≈1.41,
≈1.41,![]() ≈1.73.
≈1.73.

【答案】教学楼AB的高度AB长13.3m.
【解析】
如图,延长HF交CD于点N,延长FH交AB于点M,由题意可得,MB=HG=FE=ND=1.6m,HF=GE=8m,MF=BE,HN=GD,MN=BD=24m,设AM=xm,则CN=xm,在Rt△AFM中,可得MF=x,在Rt△CNH中,可得HN=![]() x,根据HF=MF+HN﹣MN可得关于x的方程,解方程求得x的值,继而可求得AB的值.
x,根据HF=MF+HN﹣MN可得关于x的方程,解方程求得x的值,继而可求得AB的值.
延长HF交CD于点N,延长FH交AB于点M,如图所示,
由题意可得,MB=HG=FE=ND=1.6m,HF=GE=8m,MF=BE,HN=GD,MN=BD=24m,
设AM=xm,则CN=xm,
在Rt△AFM中,MF=![]() =x,
=x,
在Rt△CNH中,HN=![]() ,
,
∴HF=MF+HN﹣MN=x+![]() x﹣24,
x﹣24,
即8=x+![]() x﹣24,
x﹣24,
解得,x≈11.7,
∴AB=11.7+1.6=13.3m,
答:教学楼AB的高度AB长13.3m.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,要建造一个四边形花圃ABCD,要求AD边靠墙,CD⊥AD,AD∥BC,AB∶CD=5∶4,且三边的总长为20 m.设AB的长为5x m.
(1)请求AD的长;(用含字母x的式子表示)
(2)若该花圃的面积为50 m2,且周长不大于30 m,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小冬和小松正在玩“掷骰子,走方格”的游戏.游戏规则如下:(1)掷一枚质地均匀的正方体骰子(骰子六个面的数字分别是1至6),落地后骰子向上一面的数字是几,就先向前走几格,然后暂停.(2)再看暂停的格子上相应的文字要求,按要求去做后,若还有新的文字要求,则继续按新要求去做,直至无新要求为止,此次走方格结束.下图是该游戏的部分方格:
大本营 | 1 对自己说 “加油!” | 2 后退一格 | 3 前进三格 | 4 原地不动 | 5 对你的小伙伴说“你好!” | 6 背一首古诗 |
例如:小冬现在的位置在大本营,掷骰子,骰子向上一面的数字是2,则小冬先向前走两格到达方格2,然后执行方格2的文字要求“后退一格”,则退回到方格1,再执行方格1的文字要求:对自己说“加油!”.小冬此次“掷骰子,走方格”结束,最终停在了方格1.如果小松现在的位置也在大本营,那么他掷一次骰子最终停在方格6的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:①学校离小明家1000米;②小明用了20分钟到家;③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快,其中正确的有______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)如图2,当⊙P与边CD相切于点F时,求AP的长;
(2)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价150元销售,最后剩下50件按八折优惠卖出,求两批衬衫全部售完后利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点D为△ABC边BC的延长线上一点.

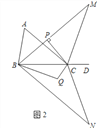
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证: ![]() ;
;
(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com