
【题目】小冬和小松正在玩“掷骰子,走方格”的游戏.游戏规则如下:(1)掷一枚质地均匀的正方体骰子(骰子六个面的数字分别是1至6),落地后骰子向上一面的数字是几,就先向前走几格,然后暂停.(2)再看暂停的格子上相应的文字要求,按要求去做后,若还有新的文字要求,则继续按新要求去做,直至无新要求为止,此次走方格结束.下图是该游戏的部分方格:
大本营 | 1 对自己说 “加油!” | 2 后退一格 | 3 前进三格 | 4 原地不动 | 5 对你的小伙伴说“你好!” | 6 背一首古诗 |
例如:小冬现在的位置在大本营,掷骰子,骰子向上一面的数字是2,则小冬先向前走两格到达方格2,然后执行方格2的文字要求“后退一格”,则退回到方格1,再执行方格1的文字要求:对自己说“加油!”.小冬此次“掷骰子,走方格”结束,最终停在了方格1.如果小松现在的位置也在大本营,那么他掷一次骰子最终停在方格6的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )
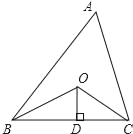
A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:

(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC = BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF = FP。
(1)在图①中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将三角板△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ。你认为(2)中猜想的BQ与AP所满足的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
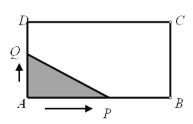
【题目】如图,长方形ABCD中,AB=4,AD=2.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为![]() (秒),在整个运动过程中,当△APQ为直角三角形时,则相应的
(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的![]() 的值或取值范围是_________.
的值或取值范围是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,校园内有两幢高度相同的教学楼AB,CD,大楼的底部B,D在同一平面上,两幢楼之间的距离BD长为24米,小明在点E(B,E,D在一条直线上)处测得教学楼AB顶部的仰角为45°,然后沿EB方向前进8米到达点G处,测得教学楼CD顶部的仰角为30°.已知小明的两个观测点F,H距离地面的高度均为1.6米,求教学楼AB的高度AB长.(精确到0.1米)参考值:![]() ≈1.41,
≈1.41,![]() ≈1.73.
≈1.73.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论:① △ODC是等边三角形;②BC=2AB;③∠AOE=135°; ④S△AOE=S△COE,其中正确的结论的个数有

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
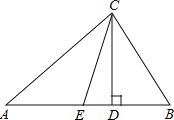
【题目】如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
(1)若∠A=30°,∠B=50°,求∠ECD的度数;
(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com