
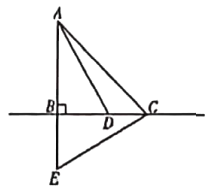
【题目】如图,在![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一点,点
上一点,点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 时,求
时,求![]() 的度数;
的度数;
![]() 点
点![]() 是
是![]() 的外心,当点
的外心,当点![]() 在直线
在直线![]() 上运动,且点
上运动,且点![]() 恰好在
恰好在![]() 内部或边上时,直接写出点
内部或边上时,直接写出点![]() 运动的路径的长,
运动的路径的长,
【答案】(1)见解析;(2):∠E=65°或25°;(3)![]()
【解析】
(1)(1)利用“边角边”证明即可;
(2)分两种情况:点D在线段BC上时和点D在BC延长线上时,利用全等三角形对应角相等,推出∠E=∠ADB,再根据等腰直角三角形的性质求出∠ACB=∠CAB=45°,根据外角性质求出∠ADB,即可解答;
(3)过点B作BF垂直AC,交AC于F,作DC边的垂直平分线交BF于点P,过点F作FG⊥BC,交BC于点G,证明BF是AC的垂直平分线,从而推出点P即为三角形CAD的外心,根据点![]() 恰好在
恰好在![]() 内部或边上,确定点
内部或边上,确定点![]() 运动的路径为BF,求BF的长即可.
运动的路径为BF,求BF的长即可.
(1)∵∠ABC=90°,
∴∠CBE=90°=∠ABC,
∵AB=CB, BE=BD,
∴ △ABD≌△CBE;
(2)当点D在线段BC上时,
∵△ABD≌△CBE,
∴∠E=∠ADB,
∵AB=CB,∠ABC=90°,
∴∠ACB=∠BAC=45°,
∴∠E=∠ADB=45°+20°=65°;
当点D在BC延长线上时,如图,
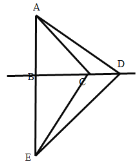
∵△ABD≌△CBE,
∴∠BEC=∠ADB,
∵AB=CB,∠ABC=90°,
∴∠ACB=∠BAC=45°,
∴∠BEC=∠ADB=45°-20°=25°;
综上:∠E=65°或25°.
(3)如图,过点B作BF垂直AC,交AC于F,作DC边的垂直平分线交BF于点P,过点F作FG⊥BC,交BC于点G,
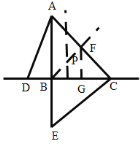
∵![]() BF⊥AC,
BF⊥AC,
∴BF是AC的垂直平分线,
∴点P即为三角形CAD的外心.
∵P为BF上一点,
由题意可知点![]() 恰好在
恰好在![]() 内部或边上,
内部或边上,
∴点![]() 运动的路径为BF,
运动的路径为BF,
∵![]()
∴![]() ,
,
∵BF是AC的垂直平分线,
∴BF=![]() ,
,
即点P的运动路径长为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数和反比例函数的图像都经过点![]() ,且
,且![]() 为双曲线上的一点,
为双曲线上的一点,![]() 为坐标平面上一动点,
为坐标平面上一动点,![]() 垂直于
垂直于![]() 轴,
轴,![]() 垂直于
垂直于![]() 轴,垂足分别是
轴,垂足分别是![]() 、
、![]() .
.
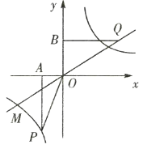
(1)写出正比例函数和反比例函数的关系式.
(2)当点![]() 在直线
在直线![]() 上运动时,直线
上运动时,直线![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 与
与![]() 的面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
的面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=4![]() ,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
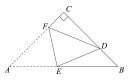
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科普小组有5名成员,身高(单位:cm)分别为:160,165,170,163,172,把身高160 cm的成员替换成一位165 cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数变小,方差变小B.平均数变大,方差变大
C.平均数变大,方差不变D.平均数变大,方差变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同型号的甲、乙两辆车加满气体燃料后均可行驶210km.它们各自单独行驶并返回的最远距离是105km.现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )
A.120kmB.140kmC.160kmD.180km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC,若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由;
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
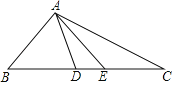
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车经营店销售![]() 型,
型,![]() 型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
|
| |
进货价格(元/辆) | 1000 | 1100 |
销售价格(元/辆) |
| 1500 |
今年经过改造升级后,![]() 型车每辆销售价比去年增加400元.已知
型车每辆销售价比去年增加400元.已知![]() 型车去年1月份销售总额为3.6万元,今年1月份
型车去年1月份销售总额为3.6万元,今年1月份![]() 型车的销售数量与去年1月份相同,而销售总额比去年1月份增加
型车的销售数量与去年1月份相同,而销售总额比去年1月份增加![]() .
.
(1)若设今年1月份的![]() 型自行车售价为
型自行车售价为![]() 元/辆,求
元/辆,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)该店计划8月份再进一批![]() 型和
型和![]() 型自行车共50辆,且
型自行车共50辆,且![]() 型车数量不超过
型车数量不超过![]() 型车数量的2倍,应如何进货才能使这批自行车获利最多?
型车数量的2倍,应如何进货才能使这批自行车获利最多?
(3)该店为吸引客源,准备增购一种进价为500元的![]() 型车,预算用8万元购进这三种车若干辆,其中
型车,预算用8万元购进这三种车若干辆,其中![]() 型与
型与![]() 型的数量之比为
型的数量之比为![]() ,则该店至少可以购进三种车共多少辆?
,则该店至少可以购进三种车共多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
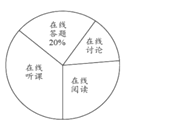
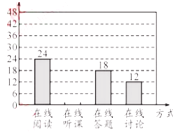
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生![]() 人,请你估计该校对在线阅读最感兴趣的学生人数.
人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com