
����Ŀ�����⣺��ͼ���ڡ�ABD�У�BA��BD����BD���ӳ�����ȡ��E��C������AEC��ʹEA��EC������BAE��90�㣬��B��45�㣬���DAC�Ķ�����
�𰸣���DAC��45��
˼������1����������ϡ����⡱�е���������B��45�㡱ȥ���������������䣬��ô��DAC�Ķ�����ı���˵�����ɣ�
��2����������ϡ����⡱�е���������B��45�㡱ȥ�����ٽ�����BAE��90�㡱��Ϊ����BAE��n�㡱�������������䣬���DAC�Ķ�����
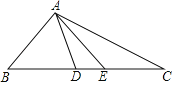
���𰸡���1����DAC�Ķ�������ı䣬ֵΪ45�㣻��2��![]() n�㣮
n�㣮
��������
��1�����ݵ��������ε����ʵõ���AED��2��C������á�DAE��90��-��BAD��90��-��45��+��C����45�㩁��C�����ɢ٣��ڼ��ɵõ����ۣ�
��2�����ABC��m�㣬���������ε��ڽǺͶ����͵��������ε����ʼ��ɵõ����ۣ�
�⣺��1����DAC�Ķ�������ı䣻
��EA��EC��
���AED��2��C����
�ߡ�BAE��90�㣬
���BAD��![]() [180�㩁��90�㩁2��C��]��45��+��C��
[180�㩁��90�㩁2��C��]��45��+��C��
���DAE��90�㩁��BAD��90�㩁��45��+��C����45�㩁��C����
���������ã���DAC����DAE+��CAE��45�㣻
��2�����ABC��m�㣬
���BAD��![]() ��180�㩁m�㣩��90�㩁
��180�㩁m�㣩��90�㩁![]() m�㣬��AEB��180�㩁n�㩁m�㣬
m�㣬��AEB��180�㩁n�㩁m�㣬
���DAE��n�㩁��BAD��n�㩁90��+![]() m�㣬
m�㣬
��EA��EC��
���CAE��![]() ��AEB��90�㩁
��AEB��90�㩁![]() n�㩁
n�㩁![]() m�㣬
m�㣬
���DAC����DAE+��CAE��n�㩁90��+![]() m��+90�㩁
m��+90�㩁![]() n�㩁
n�㩁![]() m�㣽
m�㣽![]() n�㣮
n�㣮


 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������ӵ궼���ۡ��ƽ�1�š��������ӣ��ڼ꣬�����ӵļ۸�Ϊ 5Ԫ / kg�����һ�ι���2 kg ���ϵ����ӣ����� 2 kg ���ֵ����ӵļ۸��8�ۣ����ҵ꣬����һ�ι�������ӵ������Ƕ��٣��۸��Ϊ4.5 Ԫ / kg��
��1���������⣬��д�±���

��2����һ�ι������ӵ�����Ϊ![]() kg��
kg��![]() ��. �ڼ깺��ĸ������Ϊ
��. �ڼ깺��ĸ������Ϊ![]() Ԫ�����ҵ깺��ĸ�����Ϊ
Ԫ�����ҵ깺��ĸ�����Ϊ![]() Ԫ���ֱ���
Ԫ���ֱ���![]() ��
��![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��3�� ����ͬһ����һ�ι������ӵĸ�������36Ԫ�������ɹ�������______ kg.����ͬһ����һ�ι�������10 kg�������ٸ�������________Ԫ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
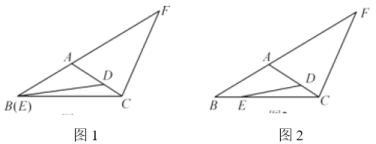
��![]() �ֱ���AC��BC���ϵĶ��㣬F��BA�ӳ����ϵĵ㣬
�ֱ���AC��BC���ϵĶ��㣬F��BA�ӳ����ϵĵ㣬![]() ��
��
��1����ͼ1������E���B�غ�ʱ����֤��![]() ��
��
��2����ͼ2����![]() ����
����![]() ��ֵ���ú�
��ֵ���ú�![]() ��
��![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��3����![]() ��
��![]() ��
��![]() ��ֱ��д��
��ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
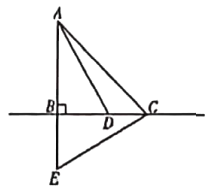
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬��
��һ�㣬��![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ������
������![]() ��
��
![]() ��֤:
��֤:![]() ��
��
![]() ��
��![]() ʱ����
ʱ����![]() �Ķ�����
�Ķ�����
![]() ��
��![]() ��
��![]() �����ģ�����
�����ģ�����![]() ��ֱ��
��ֱ��![]() ���˶����ҵ�
���˶����ҵ�![]() ǡ����
ǡ����![]() �ڲ������ʱ��ֱ��д����
�ڲ������ʱ��ֱ��д����![]() �˶���·���ij���
�˶���·���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڱ߳��ֱ�Ϊ![]() ��1�ľ���ֽƬ�����ĸ�����������ֽƬ������ֽƬ�������ּ��������ĵ����������У�����һ�����������ε������������������е�_____������ţ���
��1�ľ���ֽƬ�����ĸ�����������ֽƬ������ֽƬ�������ּ��������ĵ����������У�����һ�����������ε������������������е�_____������ţ���
��![]() ����1����
����1����![]() ��1����
��1����![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() �DZ�
�DZ�![]() ��һ����(����
��һ����(����![]() ��
��![]() �غ�)����
�غ�)����![]() ���ڵ�ֱ���۵�
���ڵ�ֱ���۵�![]() ����
����![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ����
����![]() ��ֱ����������
��ֱ����������![]() Ϊֱ�DZ�ʱ����
Ϊֱ�DZ�ʱ����![]() �ij�Ϊ____��
�ij�Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
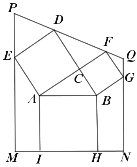
����Ŀ�����ɶ��������ƾõ���ʷ����������ܶ��˵���Ȥ��1955��ϣ����������ö�Թ���ͼΪ��������Ʊ����ν����ͼ��ָ��ֱ�������ε�����Ϊ�������������ι��ɣ���������֤���ɶ�������ͼ�Ĺ���ͼ�У���֪![]() ��
��![]() ��
��![]() .���ı���
.���ı���![]() �������
�������![]() ��
��![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() �Ľ��㣮��ô
�Ľ��㣮��ô![]() �ij�����(����)
�ij�����(����)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
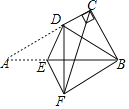
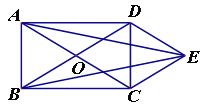
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��DE��AC��CE��BD.
��1����֤���ı���OCEDΪ���Σ�
��2������AE��BE��AE��BE�������˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com