
分析 (1)先求出∠MPC=∠ABC=90°,再根据tan∠MCP=tan∠ACB,得出$\frac{MP}{PC}$=$\frac{AB}{BC}$,$\frac{x}{4-2x}$=$\frac{3}{4}$,求出x即可;
(2)根据题意画出图形,即可得出x的取值范围;
(3)根据S△ABC=6,点O是对角线AC的中点,得出S△OBC=$\frac{1}{2}$S△ABC=3,分三种情况讨论:①当0<x≤$\frac{6}{5}$时,设OB与QM的交点为E,根据$\frac{QE}{QB}$=$\frac{BC}{AB}$得出QE=$\frac{4}{3}$x,根据y=S矩形BPMQ-S△BEQ代入计算即可;②当$\frac{3}{2}$≤x<2时,设OC与PM的交点为F,根据$\frac{PF}{PC}$=$\frac{AB}{BC}$,得出PF=$\frac{3}{4}$(4-2x),根据y=S△BOC-S△PCF代入计算即可;③当2<x<3时,设OC与PM的交点为G,根据$\frac{PG}{PC}$=$\frac{AB}{BC}$,得出PG=$\frac{3}{4}$(2x-4),根据y=S△BOC-S△PCG代入计算即可;
(4)①当0<x≤1时,此时直线AM经过BC的中点N,根据PM∥AB,得出$\frac{PM}{AB}=\frac{PN}{BN}$,$\frac{x}{3}=\frac{2-2x}{2}$,求出x;
②当1<x≤2时,此时直线AM经过CD的中点E.过点E作EF⊥AB,垂足为点F,根据EF∥QM,得出$\frac{AQ}{AF}$=$\frac{QM}{EF}$,$\frac{3-x}{\frac{3}{2}}$=$\frac{2x}{4}$,求出x,当2<x≤4时,PM>$\frac{12}{7}$,直线AM不再经过点E.
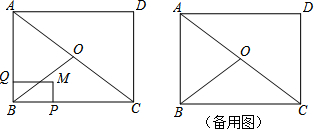
解答 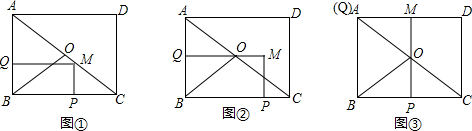 解:(1)如图①,
解:(1)如图①,
∵在矩形ABCD中,
∴∠ABC=90°.
∵∠MPC=∠ABC=90°,
∴tan∠MCP=tan∠ACB.
∴$\frac{MP}{PC}$=$\frac{AB}{BC}$,
∴$\frac{x}{4-2x}$=$\frac{3}{4}$,
∴x=$\frac{6}{5}$;
(2)如图②、③,x的取值范围是$\frac{3}{2}$<x<3;
(3)∵在矩形ABCD中,
∴S△ABC=$\frac{1}{2}$×4×3=6.
∵点O是对角线AC的中点,
∴S△OBC=$\frac{1}{2}$S△ABC=3.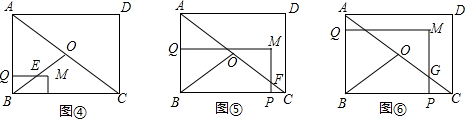 ①当0<x≤$\frac{6}{5}$时,如图④,设OB与QM的交点为E.
①当0<x≤$\frac{6}{5}$时,如图④,设OB与QM的交点为E.
∵tan∠QBE=tan∠CAB,
∴$\frac{QE}{QB}$=$\frac{BC}{AB}$.
∴$\frac{QE}{x}$=$\frac{4}{3}$.
∴QE=$\frac{4}{3}$x.
∴y=S矩形BPMQ-S△BEQ=x•2x-$\frac{1}{2}$x•$\frac{4}{3}$x=$\frac{4}{3}$x2.
②当$\frac{3}{2}$≤x<2时,如图⑤,设OC与PM的交点为F.
∵tan∠BCA=tan∠PCF,
∴$\frac{PF}{PC}$=$\frac{AB}{BC}$.
∴$\frac{PF}{4-2x}$=$\frac{3}{4}$.
∴PF=$\frac{3}{4}$(4-2x).
∴y=S△BOC-S△PCF=3-$\frac{1}{2}$•$\frac{3}{4}$(4-2x)2=-$\frac{3}{2}$x2+6x-3.
③当2<x<3时,如图⑥,设OC与PM的交点为G.
∵tan∠BCA=tan∠PCG,
∴$\frac{PG}{PC}$=$\frac{AB}{BC}$.
∴$\frac{PG}{2x-4}$=$\frac{3}{4}$.
∴PG=$\frac{3}{4}$(2x-4).
∴y=S△BOC-S△PCG=3-$\frac{1}{2}$•$\frac{3}{4}$(2x-4)2=-$\frac{3}{2}$x2+6x-3.
综合所述,y与x之间的函数关系式为y=$\left\{\begin{array}{l}{\frac{4}{3}{x}^{2}(0<x≤\frac{6}{5})}\\{-\frac{3}{2}{x}^{2}+6x-3(\frac{3}{2}≤x<2)}\\{-\frac{3}{2}{x}^{2}+6x-3(2<x<3)}\end{array}\right.$;
(4)x=$\frac{3}{4}$或x=$\frac{12}{7}$.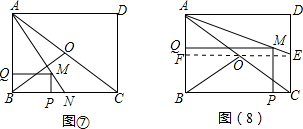 ①当0<x≤1时,如图⑦,此时直线AM经过BC的中点N.
①当0<x≤1时,如图⑦,此时直线AM经过BC的中点N.
∵PM∥AB,
∴△PMN∽△BAN.
∴$\frac{PM}{AB}=\frac{PN}{BN}$.
∴$\frac{x}{3}=\frac{2-2x}{2}$.
∴x=$\frac{3}{4}$.
②当1<x≤2时,如图(8),此时直线AM经过CD的中点E.过点E作EF⊥AB,垂足为点F.
∵EF∥QM,
∴△AMQ∽△AEF.
∴$\frac{AQ}{AF}$=$\frac{QM}{EF}$,
∴$\frac{3-x}{\frac{3}{2}}$=$\frac{2x}{4}$
∴x=$\frac{12}{7}$.
当2<x≤4时,PM>$\frac{12}{7}$,直线AM不在经过点E.
点评 此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、矩形的性质、三角函数等,关键是根据题意画出图形,作出辅助线,注意分类讨论.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
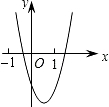 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx-$\frac{b}{2a}$与反比例函数y=$\frac{ab}{x}$在同一坐标系内的大致图象是( )
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx-$\frac{b}{2a}$与反比例函数y=$\frac{ab}{x}$在同一坐标系内的大致图象是( )| A. | 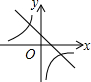 | B. | 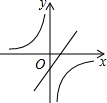 | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com