
【题目】如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.延长DA交⊙O于点F,连接FC,FC与AB相交于点G,连接OC.
(1)求证:CD=CE;
(2)若AE=GE,求证:△CEO是等腰直角三角形.

【答案】证明见解析.
【解析】
(1)连接AC,根据切线的性质和已知得:AD∥OC,得∠DAC=∠ACO,根据AAS证明△CDA≌△CEA(AAS),可得结论;
(2)介绍两种证法:
证法一:根据△CDA≌△CEA,得∠DCA=∠ECA,由等腰三角形三线合一得:∠F=∠ACE=∠DCA=∠ECG,在直角三角形中得:∠F=∠DCA=∠ACE=∠ECG=22.5°,可得结论;
证法二:设∠F=x,则∠AOC=2∠F=2x,根据平角的定义得:∠DAC+∠EAC+∠OAF=180°,则3x+3x+2x=180,即得出结论.
证明:(1)连接AC,

∵CD是⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴∠DCO=∠D=90°,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OC=OA,
∴∠CAO=∠ACO,
∴∠DAC=∠CAO,
∵CE⊥AB,
∴∠CEA=90°,
在△CDA和△CEA中,
∵ ,
,
∴△CDA≌△CEA(AAS),
∴CD=CE;
(2)证法一:连接BC,
∵△CDA≌△CEA,
∴∠DCA=∠ECA,
∵CE⊥AG,AE=EG,
∴CA=CG,
∴∠ECA=∠ECG,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CE⊥AB,
∴∠ACE=∠B,
∵∠B=∠F,
∴∠F=∠ACE=∠DCA=∠ECG,
∵∠D=90°,
∴∠DCF+∠F=90°,
∴∠F=∠DCA=∠ACE=∠ECG=22.5°,
∴∠AOC=2∠F=45°,
∴△CEO是等腰直角三角形;
证法二:设∠F=x,则∠AOC=2∠F=2x,
∵AD∥OC,
∴∠OAF=∠AOC=2x,
∴∠CGA=∠OAF+∠F=3x,
∵CE⊥AG,AE=EG,
∴CA=CG,
∴∠EAC=∠CGA,
∵CE⊥AG,AE=EG,
∴CA=CG,
∴∠EAC=∠CGA,
∴∠DAC=∠EAC=∠CGA=3x,
∵∠DAC+∠EAC+∠OAF=180°,
∴3x+3x+2x=180,
x=22.5°,
∴∠AOC=2x=45°,
∴△CEO是等腰直角三角形.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图8,AB两地之间有一座山,以前从A地到B地需要经过C地.现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km;参考数据:![]() ≈1.41,sin53°≈0.80,cos53°≈0.60)
≈1.41,sin53°≈0.80,cos53°≈0.60)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为![]() .
.
(1)如图1,若点B 在x轴正半轴上,点![]() ,
,![]() ,
,![]() ,求点B坐标;
,求点B坐标;
(2)如图2,若点B 在x轴负半轴上,![]() 轴于点E,
轴于点E,![]() 轴于点F,
轴于点F,![]() ,MF交直线AE于点M,若点
,MF交直线AE于点M,若点![]() ,BM=5,求点M坐标.
,BM=5,求点M坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的三角形中,不是直角三角形的是( )
A.∠A-∠B=∠CB.∠A:∠B:∠C=3: 4: 7
C.∠A=2∠B=3∠CD.∠A=9°,∠B=81°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=![]() ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=![]() ,y=
,y=![]() .
.
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=![]() ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
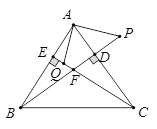
求证:(1)AP=AQ ;
(2)AP⊥AQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC纸片沿DE折叠,使点A落在点A′处,且A′B平分∠ABC,A′C平分∠ACB,若∠BA′C=110°,则∠1+∠2=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com