
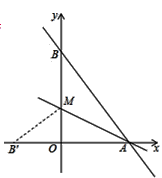
【题目】如图,直线y=-![]() x+8与x轴、y轴分别交于点A和点B,M是OB的上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B′处.
x+8与x轴、y轴分别交于点A和点B,M是OB的上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B′处.
(1)求A、B两点的坐标;
(2)求直线AM的表达式;
(3)在x轴上是否存在点P,使得以点P、M、B′为顶点的三角形是等腰二角形,若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)P(4,0)或
;(3)P(4,0)或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)求点A坐标,令y=0,得A点坐标(6,0),求点B坐标,令x=0,得A点坐标(0,8);(2)由勾股定理可得线段AB=10,由折叠的性质可知![]() ,设
,设![]() ,在
,在![]() 中,由勾股定理可得x值,求出点M坐标用待定系数法可得直线AM的表达式;(3)
中,由勾股定理可得x值,求出点M坐标用待定系数法可得直线AM的表达式;(3)
解:(1)y=-![]() x+8
x+8
令![]() 则
则![]() ,
,
令![]() ,则
,则![]()
![]()
(2)由(1)知![]() ,由勾股定理得
,由勾股定理得![]() ,
,
由折叠的性质可知![]() ,
,
设![]() ,则
,则![]()
在![]() 中,根据勾股定理得
中,根据勾股定理得![]()
解得 ![]()
![]()
设直线AM的表达式为![]()
则![]() ,解得
,解得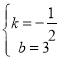
所以直线AM的表达式为![]() .
.
(3)由(2)知![]() ,可得
,可得![]()
①以点M为圆心,![]() 长为半径画圆交x轴于一点P,此时
长为半径画圆交x轴于一点P,此时![]()
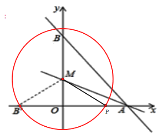
可得![]() ,所以P(4,0);
,所以P(4,0);
②以点![]() 为圆心,
为圆心,![]() 长为半径画圆交x轴于一点P,此时
长为半径画圆交x轴于一点P,此时![]()
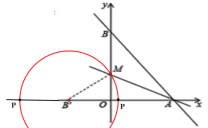
![]() 或1,所以
或1,所以![]() 或
或![]() ;
;
作线段![]() 的垂直平分线交x轴于一点P,此时
的垂直平分线交x轴于一点P,此时![]()
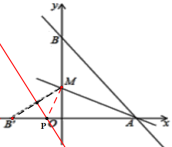
设![]() ,则
,则 ![]() ,根据勾股定理得
,根据勾股定理得![]() ,解得
,解得![]()
所以![]() .
.
综合上述,点P的坐标为P(4,0)或![]() 或
或![]() 或
或![]()


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“和谐号”高铁列车的小桌板收起时可近似看作与地面垂直,展开小桌板使桌面保持水平,其示意图如图所示.连接OA,此时OA=75 cm,CB⊥AO,∠AOB=∠ACB=37°,且桌面宽OB与BC的长度之和等于OA的长度.求支架BC的长度(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=x和y=-![]() x的图象分别为直线l1、12,过点A1(1,-
x的图象分别为直线l1、12,过点A1(1,-![]() )作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5,……,依次进行下去,则A2019的横坐标为( )
)作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5,……,依次进行下去,则A2019的横坐标为( )

A.-21007B.21008C.-21008D.-21009
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
乙种节能灯 | 35 | 50 |
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完100只节能灯后,该商场获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠MPN,依照下列步骤进行尺规作图:
(1)在射线PN上截取线段PA;
(2)分别以P,A为圆心,大于![]() PA的长为半径作弧,两弧相交于E,F两点;
PA的长为半径作弧,两弧相交于E,F两点;
(3)作直线EF,交射线PM于点B;
(4)在射线AN上截取AC=PB;
(5)连接BC.
则∠BCP与∠MPN之间的数量关系是_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数![]() 和
和![]() 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥
的图象上,PC⊥![]() 轴于点C,交
轴于点C,交![]() 的图象于点A,PC⊥
的图象于点A,PC⊥![]() 轴于点D,交
轴于点D,交![]() 的图象于点B. 当点P在
的图象于点B. 当点P在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①![]()
②![]() 的值不会发生变化
的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACD和△BCE中, AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
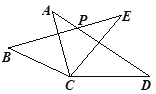
A.110°B.125°C.130°D.155°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016辽宁省葫芦岛市)甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com